前回はレイトレ合宿用に論文を読んだのですが，肝心のところが書いてなかったので，今回はレイの分類について詳細が書いてある1987年の論文を読むことにします。
毎度のごとく，誤字・誤訳が多々ありますので，間違いを指摘して頂ける場合は正しい翻訳例と共にご指摘いただけると幸いです。

Abstrct

5次元空間の細分化によって光線オブジェクトと光線境界の交差計算の数を大幅に削減するレイトレーシングの新しいアプローチについて説明します。 一般的な3D長方形ボリュームから発生し、2D立体角を通過する光線のコレクションは、5空間のハイパーキューブとして表されます。 光線の空間を区切る5Dボリュームは動的にハイパーキューブに分割され、それぞれが交差の候補であるオブジェクトのセットにリンクされます。 光線は一意のハイパーキューブに分類され、関連する候補オブジェクトセットとの交差をチェックします。ボックス、球、平面セット、凸多面体など、オブジェクト範囲のテストのためのいくつかの手法を計算します。 さらに、ソート、キャッシング、バックフェースカリングなど、アルゴリズムの指向性によって可能になる最適化を検討します。 結果は、特に複雑な環境では、このアルゴリズムが以前のレイトレーシング手法を大幅に上回ることを示しています。

1. Introduction

レイトレーシングを加速するアルゴリズムの研究における私たちの目標は、従来この方法に関連していた膨大な時間のペナルティを支払うことなく、高品質の画像を生成することです。 最近のアルゴリズムは、特に複雑な環境でほとんどの時間が費やされる場所であるため、実行される光線オブジェクト交差テストの回数を減らすことに重点を置いています。 これは、評価が簡単な関数を使用して、光線のパスに明らかにないオブジェクトをカリングすることで実現されます。

1.1 Previous Work

和訳省略

1.2 A New Approach

光線の分類アプローチは、光線の方向を含むように空間の細分化の概念を拡張するという点で、以前の研究とは大きく異なります。 その結果、非常に強力なカリング機能が得られ、経験的には、環境の複雑さに比較的影響を受けません。

このアルゴリズムの重要な特徴は、カリング機能を1回評価するだけで、レイがすべてを逃したとしても、少数ながら完全な候補オブジェクトのセットを生成できることです。 これは、関連するすべての光線の空間を等価クラス\(E_1\), \(E_2\), …, \(E_m\)に適応的に分割し、\(C_i\)は\(E_i\)で交差される可能性がある光線を含むすべてのオブジェクトを含むように候補オブジェクトセット\(C_1\), \(C_2\), …, \(C_m\)を構築することにより実現されます 。カリング関数を評価すると、特定の光線を等価クラスのメンバーとして分類し、関連する候補セットを取得することになります。 アルゴリズムは、すべての\(i\)に対して\(| C_i | \)を小さくするよう努めており、そうではないセットの影響を軽減するいくつかの新しい手法が採用されています。

2. 5-Space and Ray Classification

多くのレイトレーシングの実装では、レイは、3Dの単位方向ベクトルと結合された3Dの原点で表されます。これは、交差計算に便利な形式です。 ただし、幾何学的には、たとえば3Dの原点と2つの球面角など、5つの値だけで同じ情報を伝達できるという事実からわかるように、光線の自由度は5つしかありません。 したがって、3空間の光線を5空間の点で、より正確には5多様体\(\mathbb{R}^3 \times \mathbb{S}^2 \)の点で識別できます、ここで\(\mathbb{S}^2 \)は\(\mathbb{R}^3 \)の単位球です。したがって、光線の任意の近傍、つまり類似の原点と方向を持つ光線の集合は、\(\mathbb{R}^5\)のサブセットによってパラメータ化できます。 光線の5つの自由度すべてを利用するカリング関数を構築する際に、このようなパラメーター化を使用します。

光線分類アルゴリズムは、5つのサブタスクに分けることができます。 最後の操作を除くすべてが、少なくとも部分的に5次元で行われます。 これらは次のとおりです：

① 5D Bounding Volume:
環境と相互作用できるすべての光線に相当する5Dを含む境界サブセット\(E \subset \mathbb{R}^5\)を見つけます。

② 5D Space Subdivision:
\(E \subset \mathbb{R}^5\)をばらばらのボリュームに分割するサブセット\(E_1\), …, \(E_m\)を選択します。

③ Candiate Set Creation:
5Dボリューム\(E_i\)で表される光線のセットが与えられた場合、光線の1つと交差するすべてのオブジェクトを含む候補のセット\(C_i\)を作成します。

④ Ray Classification:
\(E\)の点に対応する光線が与えられた場合、その点を含むパーティショニング\(E_i\), …, \(E_m\)のセット\(E_i\)を見つけ、関連する候補セット\(C_i\)を返します。

⑤ Candiate Set Processing:
光線と候補オブジェクトのセット\(C_i\)が与えられると、最も近い光線とオブジェクトの交差点が存在する場合、それを決定します。

環境と交差するレイごとに、④は候補オブジェクトのセットを取得するために使用され、⑤はこのセットを使用して実際のレイとオブジェクトの交差を実行します。 後述するように、①と②が一度に実行され、④のレイ分類クエリに応じて、パーティションと候補のセットが徐々に改良されます。 理想的には、③で作成された対応する候補セットに含まれるオブジェクトの数が所定の数よりも少なくなるように、②でパーティションを探します。 これらのサブタスクについては、セクション3〜7で詳しく説明します。

2.1 Beams as 5D Hypercubes

アルゴリズムの多くは5Dボリュームを含むため、コンパクトな表現を持ち、効率的なポイント包含クエリとサブディビジョンを可能にするボリュームを選択することが重要です。 これらの理由により、5D軸に平行な平行六面体またはハイパーキューブを使用します。 これらは、X、Y、Z、U、Vのラベルを付けた5つの相互に直交する座標軸に沿った間隔を表す5つの順序付きペアとして保存されます。

光線のコレクションを表す各ハイパーキューブには、ビームと呼ばれる自然な3D表示があります。 これは、ハイパーキューブのポイントによって定義される、半無限の線、または幾何学的な意味での光線の結合によって形成される無制限の3Dボリュームです。 ビームは、光線のセットによって到達可能な3空間内のポイントを正確に構成するため、候補セットの作成において中心的な役割を果たします。 この役割の重要性を考えると、凸多面体など、簡単に表現できるビームボリュームをハイパーキューブで定義することが不可欠です。 このジオメトリは、5Dポイントを持つ光線を識別する方法によって完全に決定されます。

2.2 Rays as 5D Points

このセクションでは、\(\mathbb{R}^5\)の一意のポイントを\(\mathbb{R}^3\)の各光線に関連付ける方法について説明します。前に述べたように、光線は一意の5タプル（x、y、z、u、v）にマッピングでき、その原点とそれに続く2つの球面角度で構成されます。残念ながら、このマッピングの下でハイパーキューブに関連付けられたビームは、一般的に多面体ではありません。 これを改善するために、目的のプロパティをローカルに持ついくつかのマッピングをつなぎ合わせて、光線の空間全体をまとめます。

光線と、その中心を中心とする側面2つの軸に沿った立方体との交差を考えます。 個々の光線の方向は、この立方体の一意の交点に対応します。 式1に示すように\(\infty\)ノルムに関して光線方向ベクトル\(\rm{d}\)を正規化し、結果から\((u, v)\)を式2に示すように外挿することにより、これらのポイントに2D座標系を適用できます。

\begin{eqnarray}
{\rm{w}} = \frac{\rm d}{|| {\rm d} ||_{\infty} } = \frac{({\rm d}_x, {\rm d}_y, {\rm d}_z)}{\max (|{\rm d}_x|, |{\rm d}_y|, |{\rm d}_z|)} \tag{1}
\end{eqnarray}

\begin{eqnarray}
(u, v) =
\begin{cases}
({\rm w}_y, {\rm w}_z) & {\rm {if}} \, {\rm w}_x & = & \pm 1, & {\rm{or \, else}} \\
({\rm w}_x, {\rm w}_z) & {\rm {if}} \, {\rm w}_y & = & \pm 1, & {\rm{or \, else}} \tag{2} \\
({\rm w}_x, {\rm w}_y) & {\rm {if}} \, {\rm w}_z & = & \pm 1
\end{cases}
\end{eqnarray}

これにより、\([-1、1] \times [-1、1]\)と立方体の1つの面を通過する光線との間に1対1の対応が確立されます。立方体の面によって定義される6つの支配的な方向に光線を分割し、これらの各ドメインへのマッピングを制限することにより、6つの双連続1対1マッピングを取得します。 それぞれを、+ X、-X、+ Y、-Y、+ Z、または-Zで示される支配的な軸に関連付けます。逆マッピングまたはパラメーター化は、\(\mathbb{S}^2\)のアトラスを定義し、\([-1, 1] \times [-1, 1]\)の画像で光線方向のセットを変換します。これは、\(\mathbb{R} ^3 \times \mathbb{S}^2\)に簡単に拡張されます。 ただし、目標の1対1対応の要件を満たすために、光線の主軸を使用して、\([-1, 1] \times [-1, 1]\)の6つの「コピー」にインデックスを付けます。 与えられた光線について、この軸は軸とその最大絶対方向成分の符号によって決定されます。

UとVの間隔は、単一の立方体面を通るピラミッド立体角を定義し、X、Y、Zの間隔は長方形の3Dボリュームを定義します。 ハイパーキューブは、最大で9つの面を持つ境界のない多面体であるビームを定義します。 これは、図1aの視覚化の補助として2Dの類推とともに図1bに示されています。

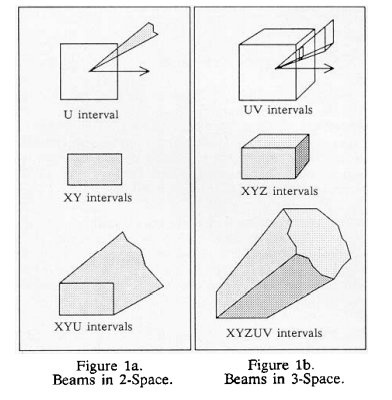
※図は，James Arvo, David Kirk, “Fast Ray Tracing by Ray Classification”, Computer Graphics, Volume 21, Number 4, July 1987より引用。

3. The 5D Bounding Volume

光線分類アルゴリズムの最初のステップは、環境に関連するすべての光線を含む\(\mathbb{R}^5\)の有界サブセットを見つけることです。 環境のすべてのオブジェクトを含む3DバウンディングボックスBを見つけることから始めます。 このようなボックスは、個々のオブジェクト範囲から簡単に取得できます。 次に、それぞれが一意の支配軸に対応し、単位球体\(\mathbb{S}^2\)の6分の1をカバーする方向に対応するハイパーキューブ\({\rm B} \times [-1, 1] \times [-1, 1]\)の6つのコピーから、目的の境界ボリュームを構築できます。

3Dバウンディングボックス\(\rm B\)も別の目的に使用されます。 アイポイントが\(\rm B\)の外側にある場合は、すべての第1世代の光線が交差するかどうかをチェックする必要があります。 交差点がない場合、レイは環境内で何もヒットしないことがわかります。 それ以外の場合、光線の原点を交差点にリセットして、光線を5Dバウンディングボリュームに移動する必要があります。

この2番目の目的のために、\(\rm B\)の代わりに他の境界ボリュームを使用できます。 たとえば、平面セット[8]は、より厳密な境界を生成することができ、それにより、環境内のすべてのオブジェクトを見逃すより多くの光線を識別します。 別の利点は、光線の再生成にあります。 光線をより狭いボリュームの境界まで押し上げることで、光線のスペースを削減し、スペースの細分化タスクをより効率的にします。

4. 5D Space Subdivision

光線を環境と交差させる場合、境界ボリュームが交差するオブジェクトのセットのみを考慮する必要があります。 セクション2の①から④のタスクの目的は、環境内のあらゆる光線に対して、これらを含むオブジェクトのセットを生成することです。 これは、シーンのコヒーレンスを活用することで効率的に行われ、類似した光線が類似したオブジェクトのセットと交差する可能性が高くなります。 光線のパラメーター化の連続性により、これは、ハイパーキューブの直径を小さくすると、ビームの光線が同様に動作する可能性が高くなることを意味します。 5D空間の細分化の役割は、対応する各ビームの光線がほぼ同じオブジェクトと交差するほど小さいハイパーキューブを生成することです。 これにより、ビームのすべての光線で候補オブジェクトの1つのセットを共有できます。

バイナリ空間細分割を使用してハイパーキューブ階層を作成し、各レベルで間隔を正確に半分に分割し、5つの軸を繰り返し循環します。 このメカニズムにより、任意の小さな直径のハイパーキューブに任意の光線を含めることができます。 ただし、潜在的な光線のまばらなサブセットのみを使用する場合、5Dバウンディングボリューム全体を細かく分割する必要はありません。 代わりに、レイトレーシング中に生成されたレイが存在する領域で発生するように細分割します。 レイの5D座標が大きすぎるハイパーキューブにあることが判明した場合にのみ、必要に応じて細分化します。 したがって、6つのバウンディングハイパーキューブから始めて、遅延評価によって階層全体を構築します。

光線によってハイパーキューブ階層に新しいパスが形成されると、2つのヒューリスティックがサブディビジョンの終了時期を決定します。 候補セットまたはハイパーキューブが固定サイズのしきい値を下回ると停止します。 小さい候補セットは、環境と交差するために関連する光線を安価にするという目標を達成したことを示しています。 ハイパーキューブサイズの制約は、候補セットを作成するコストを多くの光線で償却できるようにするために課されます。

5. Candidate Set Creation

ハイパーキューブが与えられると、候補セットを作成するタスクは、光線が交差できる環境内のすべてのオブジェクトを決定することから成ります。 これは、各オブジェクトのバウンディングボリュームをハイパーキューブで定義されたビームと比較することで実行されます。 ボリュームが交差する場合、オブジェクトはそのハイパーキューブに関して候補として分類され、候補セットに追加されます。

6つのバウンディングハイパーキューブには、環境内のすべてのオブジェクトを含む候補セットが割り当てられます。 細分化プロセスとして、階層を利用して、新しいハイパーキューブの候補セットが効率的に作成されます。 祖先の候補セット内のオブジェクトのみを再分類する必要があります。

スペース効率のために、階層内のすべての中間ハイパーキューブに候補セットを作成する必要はありません。 ハイパーキューブが1つの軸に沿って細分化されると、通常、結果のハイパーキューブのビームは実質的に重なり、親ビームに非常に似ています。 その結果、単一のサブディビジョンでは候補がほとんどなくなります。これは、新しい候補セットを作成する前に複数のサブディビジョンを実行することを示唆しています。 効果的であることがわかった戦略は、新しい候補セットを作成する前に5つの軸のそれぞれを再分割することです。 これにより、最大\(2^5\)個のハイパーキューブが同じ祖先から候補セットを導出できますが、ストレージの削減は重要です。 また、階層の遅延評価のため、すべての子孫が作成されることもまれです。

5.1 Object Classification

候補セットの作成に使用されるオブジェクト分類方法は、レイトレーサーのパフォーマンスにとって重要です。 非常に高速な方法は保守的すぎて、大きすぎる候補セットを作成する場合があります。 これにより、候補セットの作成と処理の両方で不要なオーバーヘッドが発生します。 オブジェクトを拒否する際にうまく機能する分類方法は、コストが高すぎる場合は受け入れられない場合があります。不要な光線とオブジェクトの交差チェックを回避するために使用されるオブジェクト範囲と同様に、メソッドのコストとその精度の間で妥協が必要です[17]。次のサブセクションでは、独立してまたは組み合わせて使用できる3つのオブジェクト分類手法のトレードオフについて説明します。次のサブセクションでは、独立してまたは組み合わせて使用できる3つのオブジェクト分類手法のトレードオフについて説明します。

5.1.1 Classifying Objects with LP

最初に説明するオブジェクト分類方法では、線形計画法を使用してオブジェクトとビームの交差をテストし、オブジェクトを凸多面体で囲む必要があります。 多面体のバウンディングボリュームは、その頂点リストまたはオブジェクトの凸包によって簡単に表されます。 ビーム自体が多面体であるため、オブジェクト分類の問題は2つの多面体間の交差のテストになります。 これは、ハルポイント[12]を使用して線形プログラムとして簡単に表現され、シンプレックス法[13]を使用して解かれます。 結果は、このタイプの境界ボリュームの正確な分類スキームです。 つまり、ビームの一部の光線がその境界多面体と交差する場合にのみ、オブジェクトはハイパーキューブの候補として分類されます。

残念ながら、私たちの経験では、線形計画法を解くために必要な計算が非常に高く、主要なオブジェクト分類方法としての使用が不可能であることが示されています。 ビームから遠く離れているか内部にあるオブジェクトの非常に頻繁なケースを処理するのは非常に複雑です。 それでも、おおよそのオブジェクト分類方法の有効性をテストおよび評価するための便利なツールです。

5.1.2 Classifying Objects with Planes

線形計画法アプローチは、ビームとオブジェクトの境界多面体の間に分離面が存在する場合にのみ、候補セットからオブジェクトを拒否します。 これは、複数のプレーンを直接テストし、プレーンがセパレーターでない場合にオブジェクトを候補として分類する、より単純なアプローチを示唆しています。

すべてのビームには、特にテストに適した複数の平面があり、それぞれが正の半空間にあります。 これらの平面の4つは、UVピラミッドの面に平行であり、ハイパーキューブの適切なXYZ極値に変換されます。 XYZハイパーキューブ範囲の面を含む最大3つ以上がビームの「背後」にあります。オブジェクトの境界多面体のすべての頂点がこれらの平面のいずれかの負の半空間にあることが判明した場合、オブジェクトはリジェクトされます。すべてが少なくとも1つの座標軸に平行であるため、半空間テストはこれらの平面の性質によって大幅に簡素化されます。

この方法は高速で保守的で、実際にビームと交差するオブジェクトを拒否しません。 また、オブジェクトは、たとえば、境界の多面体がビームと交差せずにU平面とV平面の両方と交差する場合、誤って候補として分類されるため、近似値となります。

5.1.3 Classifying Objects with Cones

オブジェクト分類の別のアプローチでは、球を使用してオブジェクトをバインドし、円錐を使用してビームを近似します。 これは、レイトレーシングでのコーンの以前の使用に似ています。 Amanatides [1]は、エリアサンプリングの方法としてコーンを使用し、正確で安価なアンチエイリアシングを提供することを説明しました。 Kirk [9]は、適切なテクスチャフィルタリングアパーチャを計算し、バンプマップサーフェスのアンチエイリアシングを改善するためのツールとしてコーンを使用しました。 私たちの文脈では、円錐は球体の範囲で区切られたオブジェクトの分類に非常に効果的であることが証明されています。

ハイパーキューブの候補セットを作成するには、ユニット軸ベクトル\(\rm W\)、広がり角\(\theta\)、およびハイパーキューブのビームを完全に含む頂点Pで指定されたコーンを作成します。 この円錐がオブジェクトの球体範囲と交差しない場合、オブジェクトは候補セットから省略されます。 円錐と球の交差の計算の詳細は、[1]と[9]の両方に記載されています。 セクション2.2で説明したものの逆マッピングを定義する式3の関数Fを使用して、以下に円錐の構成を説明します。

\begin{eqnarray}
{\rm F}(u, v) =
\begin{cases}
(1, u, v) & {\rm {if}} & +X & {\rm {is}} \, {\rm {dominant}} \\
(-1, u, v) & {\rm {if}} & -X & {\rm {is}} \, {\rm {dominant}} \\
(u, 1, v) & {\rm {if}} & +Y & {\rm {is}} \, {\rm {dominant}} \\
(u, -1, v) & {\rm {if}} & -Y & {\rm {is}} \, {\rm {dominant}} \\
(u, v, 1) & {\rm {if}} & +Z & {\rm {is}} \, {\rm {dominant}} \\
(u, v, -1) & {\rm {if}} & -Z & {\rm {is}} \, {\rm {dominant}}
\end{cases} \tag{3}
\end{eqnarray}

円錐軸ベクトル\(\rm W\)は、超立方体の主軸とその\(\rm U\)および\(\rm V\)間隔（umin、umax）および（vmin、vmax）のみに依存します。 これは、ベクトル\(\rm A\)と\(\rm B\)の間の角度を2等分することで構成されます。これは、式4と5で与えられます。

\begin{eqnarray}
{\rm A} = {\rm F}({\rm {umin}}, {\rm {vmax}}) \tag{4}
\end{eqnarray}

\begin{eqnarray}
{\rm B} = {\rm F}({\rm {umax}}, {\rm {vmin}}) \tag{5}
\end{eqnarray}

コーンの広がり角を見つけるには、式6と7を使用してベクトル\(\rm C\)と\(\rm D\)を構築します。次に、式8に示すように\(\theta\)を計算します。

\begin{eqnarray}
{\rm C} = {\rm F}({\rm {umin}}, {\rm {vmin}}) \tag{6}
\end{eqnarray}

\begin{eqnarray}
{\rm D} = {\rm F}({\rm {umax}}, {\rm {vmax}}) \tag{7}
\end{eqnarray}

\begin{eqnarray}
\theta = \max( {\rm A} \angle {\rm W}, {\rm B} \angle {\rm W}, {\rm C} \angle {\rm W}, {\rm D} \angle {\rm W}) \tag{8}
\end{eqnarray}

軸と広がり角がわかれば、円錐の頂点Pは、超立方体の\(\rm XYZ\)間隔で定義される3D矩形ボリューム\(\rm R\)で決まります。 ポイント\(\rm P\)は、コーンが負のコーン軸方向に\(\rm R\)の境界を最小の球体\(\rm R\)を完全に含むまで\(\rm R\)の重心を移動することにより配置されます。\(\rm P\)の結果の式は式9で与えられます。ここで、\({\rm R}_0\)および\({\rm R}_1\)はRの最小極値と最大極値です.

\begin{eqnarray}
{\rm P} = \frac{{\rm R}_0 + {\rm R}_1}{2} – {\rm W} \frac{|| {\rm R}_0 – {\rm R}_1 ||_2}{2 \sin \theta} \tag{9}
\end{eqnarray}

コーンは、ハイパーキューブのすべての潜在的な候補を分類するために使用され、ハイパーキューブごとに1回だけ構築されます。 円錐とオブジェクトの境界球との比較は高速であるため、遠隔ミスのコストは低くなります。 これにより、セクション5で説明したスペース節約対策である、まれな候補リスト作成のペナルティが軽減されます。オブジェクトに適用された線形変換Mは、その境界球の修正にも使用できます。 球の中心をMで変換し、その半径を\(|| {\rm M} ||_2\)でスケーリングする 、変換されたオブジェクトを含むことが保証された新しい球を取得します。 行列2ノルムは\(\sqrt {\rho({\rm M}^{\rm T}{\rm M})}\) [11]で与えられます。ここで、\(\rho\)はスペクトル半径で、行列の最大絶対固有値です。\({\rm M}^{\rm T}{\rm M}\)がスパースの場合、固有値 計算は非常に簡単です。 powerメソッドなどの対話型手法は、残りのケースに使用できます[5]。

6. Ray Classification

すべての光線と環境の交差の計算は、光線の分類から始まります。これは、光線に相当する5Dを含むハイパーキューブを見つけます。 これには、レイを5Dポイントにマッピングし、このポイントを含むリーフに到達するまで、レイの主軸でインデックス付けされた境界ハイパーキューブから始めて、ハイパーキューブ階層をトラバースする必要があります。 階層の遅延評価のため、このトラバーサルの多くは、別のレイに代わってそのようなパスがまだ構築されていない場合、レイを含む十分に小さいハイパーキューブで終了する新しいパスを作成するという副作用があります。 リーフハイパーキューブに関連付けられた候補セットが空の場合、レイが何も交差しないことが保証されます。 それ以外の場合は、次のセクションで説明するようにこのセットを処理します。

7. Candidate Set Processing

光線の分類によって特定の光線の候補オブジェクトのセットが生成されると、このセットを処理して、存在する場合に最も近い交差点をもたらすオブジェクトを決定する必要があります。 この検索を最適化するために、粗い交差点チェックにオブジェクト境界ボリュームを引き続き使用します。 また、境界ボリュームが既知のオブジェクト交差を超えてレイと交差するオブジェクトも拒否します。 これにより、光線とオブジェクトの交差計算の数をさらに減らすことができますが、候補セットのすべての境界ボリュームに対して光線をテストする必要があります。

特定のビームのすべての光線が同じ主軸を共有するという事実を利用することで、この後者の要件を削除できます。 候補セットのオブジェクトをこの軸に沿った最小範囲でソートし、昇順に処理することにより、範囲全体が既知の交差点を超える候補に到達した場合、リストの末尾を無視できます。 これは、レイがリストの先頭近くのオブジェクトと交差する場合に、境界ボリュームチェックの数を大幅に削減できるため、非常に大きな利点です。たとえば、図2では、最初の2つのオブジェクトのみがテストされます。これは、後続のすべてのオブジェクトが既知の交差点を超えて並ぶことが保証されているためです。 5D空間の細分化が始まる前に、関連する支配軸に沿って6つの境界ハイパーキューブの候補セットをソートすることにより、追加のオーバーヘッドなしで、すべての後続の候補セットに正しい順序を継承できます。 オブジェクト境界ボックスは、これらの初期候補セットのソートに使用される6つのキーを提供します。

※図は，James Arvo, David Kirk, “Fast Ray Tracing by Ray Classification”, Computer Graphics, Volume 21, Number 4, July 1987より引用。

8. Backface Culling

バックグラウンドカリングは、コンピューターグラフィックス[10]の分野で一般的な手法ですが、直接視線内にないポリゴンは、シャドウ、反射、 と透明性。 ただし、ハイパーキューブの候補セットを作成するときは、不透明なソリッドの一部であり、ビームのすべての光線に対して背面を向いているポリゴンを削除することが適切です。 コーンで分類する場合、式10が満たされると、この後者の基準が満たされます。ここで、\(\rm N\)はポリゴンの正面法線、\(\rm W\)はコーン軸、\(\theta\)はコーンの広がり角です。

\begin{eqnarray}
{\rm N} \cdot {\rm W} > \sin \theta \tag{10}
\end{eqnarray}

この手法を使用すると、同じ体積の空間を反対方向に向かう光線を、完全にばらばらのポリゴンセットに対してテストできます。 ほとんどのハイパーキューブのほぼ半分の候補を削除することにより、バックフェースカリングは候補セットの作成と処理の両方を大幅に加速します。

9. Image Coherence and Cachsing

画像のコヒーレンスにより、画像空間内の2つの隣接するサンプルは、非常に類似した光線ツリーを生成する傾向があります。 これは、特定の世代の連続する光線が同じビームの要素になる傾向があることを意味します。 各世代の最近参照されたハイパーキューブをキャッシュし、このキャッシュに対して新しいレイを最初にチェックすることにより、この事実を非常に有利に使用します。 光線が含まれている場合、それはキャッシュヒットであり、ハイパーキューブ階層を再走査することなく、前の候補セットが即座に返されます。 それ以外の場合は、走査によってレイを分類し、新しいハイパーキューブと候補セットでキャッシュを更新します。 階層トラバーサルは非常に効率的ですが、ハイパーキューブ内のポイントラインに必要な比較は10の比較、つまり十分に短いショートカットのみであることを確認することです。

関連するキャッシュ手法は、シャドウ専用に使用されます。 最も近い交差点を計算する必要がないため、光源のサンプリングに使用される光線は特別です。 光線の原点と光源との交差点の間に不透明なオブジェクトが存在するかどうかを判断するだけで十分です。 3空間の特定のポイントがシャドウ内にある場合、近くのポイントは同じオブジェクトによってシャドウされる可能性があります。 シャドウキャッシュは、次のシャドウ計算の一部として、各光源に関してシャドウを投影する最後のオブジェクトを単に記録し、そのオブジェクトを最初にチェックします。

10. Candiate Set Truncation

バウンディングボリュームのみに基づいて、あるオブジェクトが別のオブジェクトをオクルードするタイミングを決定できないため、候補セットには、バウンディングボリュームがビームと交差するすべてのオブジェクトが含まれている必要があります。 したがって、非常に狭いビームでも、大きな候補セットを生成できます。 ソートにより、遠く離れたオクルードされたオブジェクトがテストされないことが保証されるため、これは候補セットの処理に問題をもたらしません。 ただし、特定のオブジェクトを含む候補セットの数を増やすことにより、ストレージ要件が増加します。

近くのオブジェクトによってブロックされていないレイが受けるわずかなペナルティを犠牲にして、候補セットから遠くのオブジェクトをドロップできます。 これは、残りのオブジェクトがハイパーキューブのXYZ範囲外にあるポイントでソートされた候補セットを切り捨て、このポイントを主軸に直交する切り捨て平面でマークすることによって行われます。 たとえば、図2では、これは4番目のオブジェクトの直前に発生する可能性があります。 切り捨て平面の前にオブジェクトの交差が見つからない場合にのみ、切り捨てられた候補セットの処理が異なります。 図3を参照してください。この場合、光線を切り捨て平面に再配置し、再分類し、新しい候補セットを処理します。 これは以前の3D空間分割技術[3] [4] [7]に似ていますが、切り捨てられた候補セット内で並べ替えとバックフェースカリングの明確な利点、および実質的に作業なしで遮るもののない空間領域に光線を通過させる機能を保持します。

レイが再分類された回数を示すキャッシュディメンションを追加することにより、時折の再分類手順のコストを削減します。 これにより、ハイパーキューブ階層をたどることなく、ほとんどの再分類を行うことができます。 さらに、光線を再分類すると、元の光線の原点から遠ざかるにつれて含まれるボリュームが狭くなるため、多くの場合、正味のゲインになります。 図4を参照してください。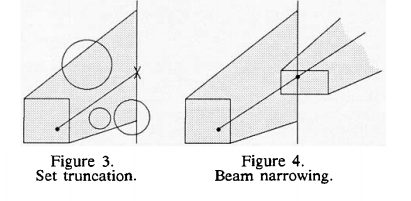
※図は，James Arvo, David Kirk, “Fast Ray Tracing by Ray Classification”, Computer Graphics, Volume 21, Number 4, July 1987より引用。

11. First-Generation Rays

第一世代の光線には2つの自由度しかないため、特性評価が容易であり、他の光線よりも頻繁に多いため、最適化が重要です。 多くのレイトレーシングの実装では、より一般的なスキャンラインまたは深度バッファアルゴリズムにより、第一世代のレイを完全に不要にします。 ただし、非常に複雑な環境では、これらのメソッドの価値は低下します。これは、最終的なイメージに寄与しないものであっても、すべてのオブジェクトにある程度の労力を費やす必要があるためです。 したがって、これらの光線に対して超線形的に実行できる光線追跡技術を調べることは価値があります。

光線分類アルゴリズムは、第一世代の光線の特殊な性質から多くの点で恩恵を受けます。 これらは縮退した3Dボリュームであるアイポイントであるため、第1世代の光線はuとvのみを使用して分類できます。 これにより、2D長方形の階層となるハイパーキューブ階層のトラバースが簡素化されるため、レイ分類の効率が向上します。 縮退したハイパーキューブに関連付けられたビームは重複しないピラミッドであるため、候補セットの作成にもメリットがあります。 したがって、候補セットはすべての下位区分で平均で半分に削減されます。 これにより、より小さい候補セットを取得することが可能になり、それにより候補セットの処理も高速化されます。 第一世代の光線に対するこれらの最適化の結果は、Warnock [16]によって導入された2D再帰的細分割アプローチに非常に類似した画像空間アルゴリズムです。

12. Summary

光線オブジェクトと光線境界の交差チェックの数を大幅に減らすことにより、光線追跡を加速する方法を説明しました。 これは、空間の細分化の概念を、光線の起点だけでなく光線の方向も利用する5Dスキームに拡張することで実現されます。 光線は、各光線との交差について効率的にテストされる候補オブジェクトの事前にソートされたセットを取得するために、5Dハイパーキューブに分類されます。 光線を環境と交差させる計算コストは非常に低くなります。これは、同様の光線が遠方のオブジェクトを選別する利点を共有し、それによりコヒーレンスを活用するためです。 この手法は、モンテカルロ積分を実行するものを含む、光線と環境の交差点に依存するすべてのアプリケーションを加速するために使用できます[2] [6]。 経験的な証拠は、特に非常に複雑な環境では、パフォーマンスが以前の方法よりも一定時間に近いことを示しています。

13. Results

和訳省略