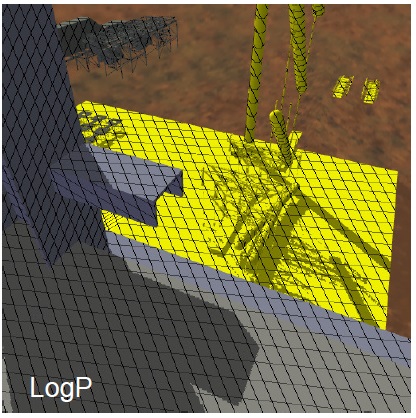
D. Brandon Lloyd氏の博士論文である,Logarithmic Perspective Shadow Mapsを適当に訳していくことにします。
前回はABSTRACTを訳しました。今回はChapter. 1を訳していきます。
日本語としては多々見苦しい点があるかと思いますが,そこはご容赦ください。
CHAPTER 1
Introduction
我々の周囲の世界の近くは主に我々が見るものを通じて伝わります。毎日,日が昇り,世界は光を浴び,人工の光を使用することによって我々は活動を続けています。光それ自身のように我々の感覚の観点としてほとんど同じくらい重要なのは世界の一部が暗闇のままであること。すなわち,シャドウです。
1.1 Importance of Shadow
和訳省略。
1.2 Shadow maps
和訳省略。
1.3 Avoiding Sampling artifacts
図1.6で示すサンプリングアーティファクトを回避するためのいくつかの方法が存在します。それらは完全にサンプリングを避けるオブジェクトベースのアプローチを使用すること,シャドウマップの解像度を増加させること,あるいはより良いサンプル分布を使用することを含みます。これらのアプローチの各々について簡潔に議論します。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p7 より引用。
1.3.1 Object-based approatches
オブジェクト空間でシャドウを計算するアプローチはサンプリングアーティファクトの影響を受けません。認知があるオブジェクト空間の手法はシャドウボリュームアルゴリズムです(Crow, 1977)。このアルゴリズムは遮蔽物の背後にあるためライトからは見えない点のボリュームを明示的に構築します。シャドウボリュームはライトから離れる方向に向かって無限遠に遮蔽物のシルエットエッジを押し出すことによって生成されます。点がシャドウ中にあるかどうかを決めるために,シャドウボリューム中にレイが入るたびにカウンタを増やし,レイがシャドウボリュームから出たときにカウンタを減らし,任意の方向に点から離れていくレイをトレースすることができます。最終的なカウンタの値が非ゼロである場合には,その点はシャドウボリュームの中にあります。グラフィックスハードウェアでは,使用される例は視点と画像中のピクセルを通過するものです。ステンシルバッファは各レイに対するカウンタを提供するのに使用されます。
シャドウボリュームアルゴリズムは3つのパスから構成されます。最初のパスでは,シーンはアンビエントライティングを伴った状態で描画されます。第2パスでは,深度バッファの書き込みが無効化されており,シャドウボリュームがフロントフェイスに対してインクリメントでバックフェースに対してデクリメントするステンシルバッファへと描画されます。最終パスでは,再度画像が描画され,このときには完全なライティング状態で,ステンシルテストは非ゼロの値を持つピクセルへの書き込みを無効化するのにつかわれます。従って,影がある領域においてアンビエントライティングは維持されます。
シャドウボリュームアルゴリズムは正確なシャドウエッジを生成しますが,いくつかの欠点を有します。シャドウボリュームはポリゴンメッシュで表現された遮蔽物を必要とします。従って,明示的なシルエットエッジを持たない,アルファテストがあるジオメトリやポイントベースの表現を持つものには使用することができません。すべてのオブジェクトベースのアプローチと同様に、シャドウボリュームアルゴリズムのパフォーマンスは、シーンの幾何学的な複雑さに非常に敏感です。個々のシャドウボリュームは大抵画面の広い領域を占めています。複雑なシーンで多くの大きなシャドウボリュームを描画することは現在のグラフィックハードウェア上でパフォーマンス低下を招きます。
1.3.2 Increasing shadow map resolution
アンダーサンプリング問題への疑う余地のないアプローチはシャドウマップの解像度を上げることです。シャドウマップ誤差の大きさはシャドウマップの解像度に比例して減少します。しかしながら,このアプローチはいくつの制限があります。大きなシャドウマップは現在のグラフィックスハードウェアの限りあるストレージ容量を圧迫します。GPU上で利用可能なメモリ量が増加する一方で,描画されたシーンの視覚的なリッチさも増加しています。高解像度のシャドウマップはテクスチャマップ,頂点データそしてシェーダなどのリッチさを提供するものとGPUのメモリを取り合わなければなりません。高解像度のシャドウマップを描画することはより多くのレンダリング作業があるため,時間がかかります。レンダリングのスピードは帯域幅のボトルネックによって制限される可能性が高いです。高解像度のシャドウマップを用いて画像を生成することはキャッシュパフォーマンスの貧弱性のために遅くなる可能性があります。観測者から遠く離れた領域はシャドウマップによってオーバーサンプルされる傾向があります。これらの領域では,メモリ上でシャドウマップクエリはキャッシュパフォーマンスを損なうまばらな空間的局所性を示します。シャドウマップの解像度が増加すると,この問題が悪化します。
1.3.3 Explicit sampling
ブルートフォースによってエイリアシングに対処するために単純にサンプル数を増やすよりも,より良いアプローチはシャドウマップのサンプルをより慎重に配置することです。理想的には,シャドウマップの解像度は各ピクセルに一致する単一のシャドウマップのサンプルを持つ画像解像度よりも大きくありません。レイトレーシング(Whitted, 1979)のようなアプローチや,イレギュラーZバッファ(Johnson & Cohen, 2004; Alia & Laine, 2004a)は正確にこの一致を確立しました。これらの双方のアプローチは,標準的なシャドウマップよりもはるかに少ないサンプルでアーティファクトフリーなエッジを生成することが可能です。レイトレーシングは,単純に遮蔽物と交差するチェックをするためにライトに向かってレイを追跡することによって,シーンにおける任意の点でシャドウを計算することができます。従って,レイトレーシングは画像中でピクセルに一致するシーン上のこれらの位置において正確にサンプルすることができます。この柔軟性のための対価があります。全部のシーンのデータベースにアクセス可能である必要があります。なぜかというと,シーンにおける任意のオブジェクトは潜在的に交差する可能性があるからです。言い換えると,レイトレーシングはリテインドモードで動作する必要があります。交差判定は高コストであるため,複雑なシーン上で実行するためには交差判定の数を減らすために離散データ構造が典型的には使用されます。複雑なモデルに対する加速のデータ構造を構築することと動的なシーン上でそれらをメンテナンスすることはかなりのオーバーヘッドを持つ可能性があります。
イレギュラーZバッファアルゴリズムは画像平面上のサンプル位置の任意のセットを用いてポリゴンをラスタライズするものです。イレギュラーZバッファを用いてシャドウマップを生成するためには,シーンは最初にカメラの視点から描画されます。アイサンプルの位置はライト空間に変換され,シャドウマップを描画するために使われます。最終的には,結果としての深度バッファはアイサンプルの位置におけるシャドウを計算するために使われます。イレギュラーZバッファは,理想的な光源についてはレイトレーシングと同じような結果を生み出します。各ポリゴンは独立して処理できるので,アルゴリズムは従来のグラフィックスパイプラインとうまく適合します。アルゴリズムの主な課題はサンプル分布の不規則性です。ライト視点からアイサンプルは非常に不均一である可能があります。これらのサンプルのインデックス作成はイレギュラーなデータ構造,例えば四分木(Aila & Laine, 2004a)や標準的なラスタライズ化に対してレギュラーグリッドが使われるよりもハードウェア上で効率的に実装するのがより難しいリストのグリッド(Johnsonら, 2005)のようなものが必要となります。通常のシャドウマップについてサンプル位置はテクセルグリッド位置によってパラメータライゼーションされる関数を用いて暗黙的に導出されます。パラメータライゼーションを用いることはサンプル位置における制約を置きますが,2つの重要な利点を持ちます―シンプルさと一貫性の高さです。サンプル位置は一定時間で計算とインデック作成することができ,レギュラーグリッド上に保存することができます。ある重要な操作,例えばフィルタリングのようなものはレギュラーグリッドを用いてより単純です。パラメータライゼーションを用いたラスタライズ化もまた並列化が容易です。サンプル間のコヒーレンスは増分計算と深度バッファ圧縮のような最適化を介してパフォーマンスを向上させるために利用することができます。現代のGPUのパフォーマンスは大きくはパラメータライゼーションによってもたらされる利点のためです。レイトレーシングにおける近年の向上は静的なシーンについて期待できる結果が示されてコーヒンレンスが利用できるということをより活用できるが,これらのアルゴリズムは依然として高解像度で適度に複雑で,動的なシーンについてGPUのパフォーマンスと立ち向かうことはできません(Waldら, 2007)。レイトレーシング(Woopら, 2005)とイレギュラーZバッファ(Johonsonら2005)を加速するためのハードウェアアーキテクチャが提案されていますが,標準のラスタライズ化と比べると,それらは効率的に実装するのにより困難です。まだ今のところ,どちらのアプローチについても実装している大規模なマーケットは存在していません。
1.3.4 Warping and partitioning
パラメータライゼーションを伴うシーンにおいてアイサンプルとライトサンプルの間の位置を正確な対応を確立することは難しい一方で,標準的なシャドウマップによって生成されるものよりもアイサンプルとライトサンプル間の分布のより良い一致を得ることが可能です。まず,シャドウマップはシャドウマップの解像度は決してみることができないシーンの部分に無駄に使われることがないので,カメラ視点で実際に見えるシーンの部分にタイトに合わせることができます(Brabecら2002b)。しかしながら,このアプローチは、まだオブジェクトが全体の視野錐台全体に表示されているビューに対してアンダーサンプリングのアーティファクトを除去するために高解像度のシャドウマップを必要とします。図1.7でこの問題を図解します。ここでは,視錐台は俯瞰のディレクショナルライトから見ています。視錐台のテーパ形状がアイサンプル位置間の間隔は,一般的には観測者からの距離で線形に増加します。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p10 より引用。
しかしながら,標準的なシャドウマップの均一パラメータを使用した時,サンプリング比率は視錐台上で一定になり,観測者の近くでアンダーサンプリングを招きます。いくつかのアルゴリズムが視錐台上の非均一なサンプリング比率を得るために提案されています。我々はこれらのアルゴリズムを主に2つのカテゴリに分けます:ワーピングとパーティショニングです。ワーピングは非均一パラメータライゼーションを用いてサンプル分布を制御します。パーティショニングは複数のシャドウマップを用いてサンプル分布上の局所的な制御を提供します。
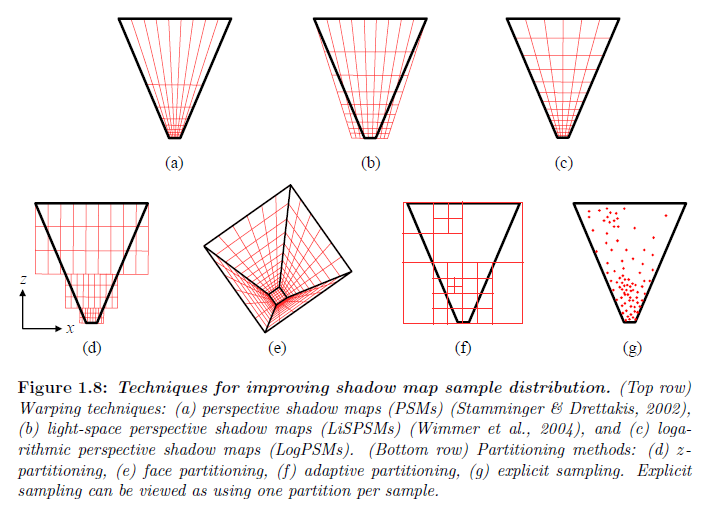
図1.8が示すのはワーピングとパーティショニングの事例です。既存するパーティショニングアルゴリズムはシャドウマップの長方形のサンプルグリッドを台形の視錐台へと歪めるために透視投影を使用しています。このワーピングは長方形のシャドウマップを埋めるためのシャドウマップ空間上の視錐台を拡大するものとしても見ることができます。射影ワーピングアルゴリズムは透視シャドウマップ(PSMs)(Stamminger & Drettakis, 2002),ライト空間透視シャドウマップ(LiSPSMs)(Wimmerら2004),そして台形シャドウマップ(TSMs)(Martin & Tan, 2004)を含みます。俯瞰のディレクショナルライトについて,これらのアルゴリズム間の主な違いはワーピングの強さを制御するパラメータが計算される方法です。これらのアルゴリズムは単に視錐台の形状に基づいており,シーン上のサーフェイスを考慮しません。このように,それらはシャドウアーティファクトを完全に排除することは保障されていません。しかしながら,実装はかなり安いです。なぜかというと,透視投影は現在のGPU上で4×4変換行列が利用でき,符号化できるので,既存のワーピングアルゴリズムはシャドウマップをレンダリングする際にカメラ行列を修正することのみが必要です。
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p11 より引用。
パーティショニングアルゴリズムはより小さなシャドウマップが局所的なサンプリング分布をよりよく制御するようにシャドウマップの解像度を複数に分けます。最も単純なパーティショニングスキームは我々がZパーティショニングと呼ぶものです。Zパーティショニングは、より小さなサブ錐台へと視点空間のz軸(視方向)に沿って視錐台を分割し,それぞれに独立したシャドウマップを(図1.8dを参照)が適用されます。複数のシャドウマップは単一ものよりも視錐台の形状を確認することができます。適応的パーティショニングアルゴリズムは必要とされるサンプル密度の局所的な変化に対応するために典型的には4分木上に配置された複数のシャドウマップを使用します。適応的手法はシーン上のサーフェイスの位置と向きを考慮にいれることができるので,より正確にできます。また,それらは高価である傾向があります。なぜかというとパーティショニングを改善することを決めるためのシーン解析のコストが追加されるからです。さらに,シーンに依存したパーティショニング技法はシンプルなものよりもより多くのシャドウマップを必要とする傾向があります。イレギュラーZバッファアルゴリズムは,サンプルごとのパーティションを使用するパーティションスキームとしても見ることができます。
ワーピングはパーティショニングと組み合わせることもできます。例えば,Zパーティショニングで生成された各サブ錐台は歪んだシャドウマップで描画することができます。適応的な技法はシーンのグローバルなワーピングの最初に適応することができます。我々がフェイスパーティショニングと呼ぶその他のテクニックは,視錐台をその面に一致する領域へ再分割し,それぞれに対して歪んだシャドウマップを適用します。
1.4 Problems with existing shadow map techniques
見て分かるように,大抵組み合わせることができる基本的なシャドウマップアルゴリズムのかなりの数のバリエーションが存在します。しかしながら,多くの技術の誤差特性はよく理解されていません。アルゴリズムのいくつかは理論的な誤差解析に基づいていますが,解析は通常特定のライト/カメラ設定に制限されています。一般的なライト位置についてのアルゴリズムの振る舞いは不完全に理解されており,使用するためのアルゴリズムがより難しくなるので,それがしばしば予期せぬ結果を招く可能性があります。これはライト位置で誤差が劇的に変化するため,特にいくつかのワーピング手法に当てはまります。いくつかの手法がシャドウマップ上のシーンの投影されたエリアを最大化するような経験則に完全に基づいています。理論的な解析の欠如は,”自分のアプリケーションにとって最も良いアルゴリズムはどれ?”,”どのぐらいのシャドウマップ解像度が必要?”,あるいは”どのくらい多くのZパーティションを使用すべきか,そしてどこでパーティションを作るべきか?”などのような開発者に対する基本的な質問の返答を難しくしています。
透視投影に基づく既存のワーピングがもつ1つの問題は,このパラメータライゼーションがアイサンプルの分布に最良一致を生成しないことです。図1.8aで見てとれるように,透視投影は視錐台に良好な適合を生成します。しかしながら,視錐台の長さに沿ってサンプル間の空間は2次的に増加しており,一方でアイサンプルの空間は線形にのみ増加します。双方の方向における空間分布は透視投影で結合されるので,ビュー方向に沿った最適なフィットのみ直交方向上のフィットを犠牲にして得ることができる(図1.8b参照)。
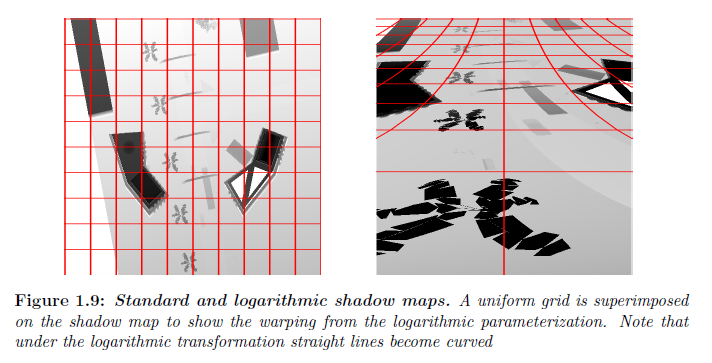
何人かの研究者(Wimmerら2004; Zhangら2006a)は視線方向に沿って線形空間分布を提供する対数パラメータライゼーションを使用することを示唆している。しかしながら,我々はリアルタイムアプリケーションについてシャドウマップを描画するために対数パラメータライゼーションを使用した公開されたアルゴリズムがないことを知っています。非線形のために,対数パラメータライゼーションが検討されていない新たな問題を招きます。図1.9に示すように,対数パラメータライゼーションは直線と平面的なサーフェイスが曲面になることを引き起こします。現在のGPUはこれらの種類のサーフェイスに対するネイティブサポートはありません。対数パラメータライゼーションはシーンを適応的にテッセレーティングすることと,プログラマブルシェーダを用いて頂点に対して対数変換を適用することによって近似することができますが,これはGPU上で頂点変換のロードが増加し,シャドウ描画コードの複雑さが増します。また対数パラメータライゼーションはフラグメントシェーダ上でブルートフォースラスタライズ化することで実装することができます。このアプローチは正確な結果を生み出すことができる一方で,実装がより複雑で,標準のラスタライズ化よりも遅くなります。さらに,平面のサーフェイス上の自己シャドウイングのアーティファクトを回避するためのテクニックは曲面に対してはうまく動作しません。
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p14 より引用。
1.5 Thesis goals
この論文は,これら2つの問題に対処することを目的とします。我々は様々なワーピングやパーティショニング方法の性能と制限をより完全な理解を提供すること目的とします。これは特定のアプリケーションのパフォーマンスと誤差要件を満たすアルゴリズムをより簡単に選択することを開発者に対して可能にします。
また,リアルタイムアプリケーションに対してシャドウマップアルゴリズムを改善するものを探索します。アルゴリズムは既存のアルゴリズムと同様のパフォーマンスと実装の複雑さを持ちますが,より少ない誤差です。誤差を減らすことは視覚的な品質を向上することについて重要だけではなく,パフォーマンスを増加させることについても重要です。シャドウマップのレンダリングはパフォーマンスは帯域制限によるものなので,ふつう高価なシェーダは含みません。少ない誤差のアルゴリズムは,より少ないシャドウマップの解像度で特定の誤差と結びつくため,より少ないストレージと帯域幅で済みます。
我々は対数パラメータライゼーションと透視パラメータライゼーションの組み合わせがそのようなアルゴリズムを生成するのに利用できることを示します。また,さらにそのようなパラメータライゼーションが既存のグラフィックスハードウェアのアーキテクチャにてこをいれる少ない追加修正でGPU上で実装できることを示します。これにより主題文を導きます。
1.5.1 Thesis statement
対数透視シャドウマップ(LogPSMs)はリアルタイムアプリケーションに対して既存のシャドウマップアルゴリズムを超える大幅な誤差削減を生み出すことができます。対数ラスタライズ化はLogPSMsをサポートするために必要とされ,現在のグラフィックスハードウェアに対する追加の修正を通して,線形ラスタライズ化と同様のパフォーマンスで実装可能です。
1.6 Overview of our approach
1.6.1 Scope
この論文では我々はハードシャドウに対して注目を制限しますが,我々の手法はソフトシャドウを生成するために使用するシャドウマップアルゴリズムに対しても有益かもしれません。我々のターゲットはリアルタイムアプリケーションであるので,少ないパーティション数(10未満)だけを必要とするシーンに非依存なアルゴリズムに焦点を当てます。これらのアルゴリズムは最も簡単で実際にやってみると最も良いパフォーマンスを保持します。特に,これが意味するのは適応的シャドウマップのようなアルゴリズムは考慮せず,シーンに非依存のアルゴリズムよりも少ない誤差を生成することができることです。最近提案された適応的シャドウマップに基づくアルゴリズムは単純なシーンにたいしてリアルタイムに近いパフォーマンスであることが報告されています(Lefohnら2007)。しかし,適応的アルゴリズムは今日のGPU上でシーン非依存のアルゴリズムを使用した単純なものと競合するのが可能なほどグラフィックスハードが十分速いと言うには難しいです。LogPSMsはより少ない誤差で単純なアルゴリズムと同じくらいのパフォーマンスを提供することを目的とします。
LogPSMsの有益性を確立するためには,最初にシャドウマップ誤差の解析を行う必要があります。我々は一般的にエイリアシングと呼ばれるギザギザのシャドウエッジを引き起こすアンダーサンプリング誤差の大きさを最小化するための方法を探求します。エイリアシング誤差は2つの部分に分解することができます:透視エイリアシングは視錐台の先細形状によるもので,投影エイリアシングはライトと目に関連するシーンにおいてサーフェイスの向きに関係します。投影エイリアシング誤差を最小化することはシーンに依存した解析と適応的技法の使用は,数多くの描画パスの実行を必要とします。それゆえ,透視エイリアシング誤差を最小化ことのみ捜索します。
我々の解析では,最悪のケースの限度を主として焦点を当てます。画像内の実際の誤差は視錐台内のシャドウの位置に依存します。対話型アプリケーションでは,視点は制限されずシーンジオメトリは任意であり,シャドウは視錐台のある一部で表示される場合があります。従って,\(L_{\infty}\)のノルムまたは最大ノルムを用いて視錐台全体上の透視エイリアシング誤差を測定します。この測定基準を用いて最悪の場合の誤差におけるシーン非依存の品質保証を与えます。
1.6.2. Logarithmic perspective parameterization
我々は透視投影としてLogPSMsパラメータライゼーションを定式化し,対数変換を1方向のみに適用します。想定するライト空間の\(y\)軸は目の視線方向に沿っていて,シャドウマップ座標は\(s\)と\(t\)によって表現されます。\(y\)軸に沿った透視投影は以下の式になります:
\[
s_p = \frac{{a_0}x+a_1}{y} \hspace{1.5cm} t_p = \frac{{a_2}y+a_3}{y} \tag{1.1}
\]
ここで,\({a_0}…{a_3}\)は定数です。この投影は\(s\)における良い空間分布を生み出すことができますが,\(t\)上の分布は\(y\)に沿った対数パラメータライゼーションを用いることによって改良することができます:
\[
t_1 = {b_0}{\rm log}({b_1}y) \tag{1.2}
\]
ここで,\(b_0\)と\(b_1\)は定数です。我々はのパラメータライゼーション変換式1.1を式1.2へと\(t_p\)へのアフィン変換(スケールと平行移動)によって\(1/({b_1}y)\)を得て,\({\rm log}(1/({b_1}y))\)を得るために,\({\rm log}\)を適用し,\({b_0}{\rm log}({b_1}y)\)を得るために\(-{b_0}\)倍します。対数透視パラメータライゼーションは以下の形式です:
\[
t_{lp} = c_{0}{\rm log}(c_{1}t_{p}+c_{2}) \tag{1.3}
\]
ここで,\(c_0\),\(c_1\)と\(c_2\)は定数です。この公式の主な利点は透視部分のパラメータライゼーションが変更を加えずに標準ぐらいフィックスパイプラインによって扱うことができることです。最も重要なことは湾曲したプリミティブをクリップする必要がないということです。対数変換をサポートするためには,ラスタライザのみ変更する必要があります(ラスタライザーのパートとして三角形のセットアップもまた変更する必要があることを含みます)。
公式化のもう1つの利点は対数透視パラメータライゼーションを使用するために既存の透視ワーピングアルゴリズムを拡張するのが容易であることです。この論文では我々はパラメータを使用するために3つの異なるアルゴリズムを拡張します:ライト空間透視シャドウマップ(LiSPSMs)(Wimmerら,2004)に似たシングルシャドウマップアルゴリズム,平行分割シャドウマップ(PSSM)(Zhangら,2006a)に似たZ分割アルゴリズム,そして透視ワープドキューブマップ(Kozlov,2004)に類似した面分割アルゴリズムです。これらのアルゴリズムのそれぞれは異なるパフォーマンスと誤差トレードオフを持ちます。全てのシングルシャドウマップアルゴリズムのように,我々のLogPSMのシングルシャドウマップはライトの方向が視線方向に対して垂直になったときに最も低い誤差を生成しますが,ライト方向が視線方向に近づくにつれて均一パラメータライゼーションにもどります。Z分割化を追加することは悪いライト設定に対する誤差を削減します。面分割アルゴリズムは若干複雑ですが,すべての光方向上で最も低い誤差を生成します。さらに方向ライトと無指向性ライトの両方に対してほとんど同じコストで使用することができます。
我々は,対数ラスタライズ化をシミュレートするためにフラグメントプログラムを用いて複雑さが変化するいくつかの環境についてこれらのアルゴリズムの有益性を実証します。我々の最適化されていないシミュレータは非常に遅いですが,それでも対話的です。しかしながら,ハードウェアアクセレレーションで,LogPSMアルゴリズムは既存のアルゴリズムと同様のパフォーマンスを保持します。
1.6.3 Logarithmic rasterization
GPU上で対数ラスタライズを実装するために,現在のハードウェアアーキテクチャへのいくつかの追加変更を提案します。我々はラスタライザ,オフセット,そして深度圧縮を変更必要があります。現在のパフォーマンスの高いGPU上でラスタライザはプリミティブによってカバーされるピクセルを計算するためにエッジ方程式を使用します。それは一般的に2つのステージで操作されます。粗いステージはカバーされたタイルのピクセルを潜在的に特定し,最終ステージは各ピクセルにおける範囲を計算します。我々は対数変換によって生成された湾曲したエッジに対するエッジ方程式を扱うためにラスタライザを拡張します。対数ラスタライザは同じタイルトラバーサルと現在のラスタライザによるカリング最適化を使用することができます。ポリゴンオフセット,典型的には自己シャドウイングを避けるために使用されます,そして深度圧縮もまた変更する必要があります。
モダンなGPUは典型的には何年にも渡る注意深い最適化とチューニングの結果になっています。我々の変更は既存のハードウェアデザインにてこ入れし,低コストで実装するのが簡単です。湾曲したエッジ方程式でラスタライズ化することは少量の追加の計算力を必要としますが,かなりの帯域幅の節約を提供することができます。従って,これらの変更は計算能力,メモリ帯域幅を上回り続けるハードウェアのトレンドとよく合います(Dally & Poulton,1998)。
1.7 Summary of results
この論文の主な結果は3つのカテゴリに分けることができます。第1にシャドウマップ手法の誤差の理論的な解析に関連する数多くの結果を得ました。第2に,この解析を使用しいてLogPSMと同じように既存手法を向上して使用することができるいくつかのアルゴリズムにたどり着きました。第3にLogPSM描画をサポートするために既存のハードウェアの変更を提案します。これらのカテゴリの各々について詳細に議論します。
1.7.1 Theoretical analysic of shadow map algorithms
我々はいくつかのシャドウマップアルゴリズムの振る舞いをより良く理解することと,既存の手法以上にLogPSMsの有益性を決定するためにいくつかのシャドウマップアルゴリズムを解析しました。具体的な結果は次のものを含ます。
- ●雑多な位置におけるポイントライトとディレクショナルライトの両方からの誤差についての方程式:以前の誤差解析は主に俯瞰のディレクショナルライトに焦点を当てています。
- ●ストレージ因子誤差測定基準:我々はストレージ因子と呼ばれるシャドウマップアルゴリズムの誤差評価の新しい測定基準を導入します。ストレージ因子はピクセル単位の画像のサイズに関係のあるシャドウマップ中のテクセルサイズです。この測定基準は双方のシャドウマップの方向の誤差を同時に考慮する間最大誤差を最小化するのを可能とします。
- ●誤差範囲:エイリアシング誤差方程式を使用して,ストレージ因子の項において異なるシャドウマップアルゴリズムに対する誤差範囲を計算します。
我々はこの誤差解析をアルゴリズムの範囲と”Z分割だけよりもよくなる面分割とZ分割の組み合わせはいつであるか?”のような質問に返答するために使用します。
1.7.2 Algorithmic results
シャドウマップエイリアシングの解析はシャドウマップアルゴリズムに対していくつかの改善を導きます。
- ●LogPSMアルゴリズム:我々は既存のシャドウマップアルゴリズムを対数透視パラメータライゼーションを組み込みために拡張する方法を示します。また我々はこれらのアルゴリズムの利益を対数ラスタライズをシミュレーションするためにフラグメントプログラムを用いて実証します。
- ●解像度再分配:シャドウマップに対して正方形のテクスチャを使用することは一般的な慣習です。しかしながら,各シャドウマップ方向における誤差は必ずしも同じではありません。分割手法について,1つのパーティションから次へのパーティションで変わる恐れがあります。我々は誤差に従ってシャドウマップ解像度を再分配することによって全体の誤差を最小化します。例として高い誤差を持つパーティションは低い誤差を持つものよりもより多くの解像度を持ちます。解像度もまた各方向における誤差に比例したシャドウマップ方向の間で分割されます。また,我々は1つの方向に向って解像度を分配するバイアスパラメータあるいはユーザーがより制御できるその他のものを提供します。
- ●ワーピングアルゴリズムに対する改善されたパラメータの選択:視錐台をまるっと覆う単一のシャドウマップとともに使用されるワーピングアルゴリズムの時に,ワーピングの強さは視線方向にライトが近づく際の異常誤差を避けるために減らされるべきです。ある設定において,現在のワーピング手法は通常のシャドウマップを超えるを誤差を生成する可能性があります。我々の誤差解析を使用してそのほかのライト位置について低い誤差を維持しつつ,より高い誤差環境設定において通常のシャドウマップより低く誤差を保つ改善されたパラメータ選択関数を定式化します。
- ●疑似近平面アルゴリズム:サーフェイスがあまりにも観測者に近いときに,ニア平面によってクリップされます。この問題を避けるために,開発者は典型的に可能な限り小さなニア平面距離の値を慣例的に選びます。しかしながら,これはシャドウマップ誤差には逆効果をもたらします。その誤差はニア平面に対するファー平面の距離比に依存します。誤差を最小化し,視錐台の占有されていない領域上の無駄なシャドウマップサンプルを避けるためには,ニア平面の距離は理想的には可能な限り大きく設定すべきです。我々はこれらの2つの相反する尺度を一致させるために疑似近クリップ平面アルゴリズムを用いてニア平面距離を設定します。Z分割位置と/またはワーピングパラメータを計算するときに視錐台全体よりも疑似近クリップ平面を超える視錐台の部分のみにおける最大誤差を最小化します。実際のニア平面と疑似近クリップ平面間の領域は依然としてシャドウマップによって覆われますが,高い誤差を有することが許可されます。疑似平面は好ましいジオメトリを含む視錐台の部分について大まかな情報でシャドウマップの最適化を提供するための方法としてユーザーに与えます。
- ●Z分割によるLogPSMの近似:対数ラスタライズ化なしのハードウェア上で,Z分割でLogPSMと同じ誤差に近づけることが可能です。誤差範囲を使用して我々は,LogPSMに対応する誤差におけるユーザーが指定した閾値に合わせるために必要なZ分割の多さはどれくらいかということを導きます。/li>
我々はまた,いくつかの実際の役に立つ考察と開発者に対して有益なシャドウマップアルゴリズムの実装も議論します。
1.7.3 Hardware support for LogPSMs
LogPSMsによって必要とされる対数ラスタライズ化は現在のグラフィックスハードウェア上ではサポートされません。対数透視パラメータライゼーションはグラフィックスパイプラインへと容易に適合するように公式化されているので,グラフィックスハードウェアは既存のグラフィックスハードウェアを増分拡張することを通じて対数ラスタライズ化をサポートするために拡張することが容易にできます。これらの拡張は次のものを含みます:
- ●非均一グリッド上でのラスタライズ化:対数ラスタライズ化によって生成される湾曲したエッジ方程式で描画することはある方向における非均一空間でのレギュラーグリッド上の線形エッジをラスタライズすることとして考えることができます。我々は非均一空間を取り扱うために均一グリッド上でラスライズ化を拡張します。このアプローチを用いて,対数ラスタライズは線形ラスタライズ化によって使用される同じ最適化を活用することができます。また,ピクセルの欠損や重複なしでメッシュの水密なラスタライズ化を提供します。
- ●ポリゴンオフセットの一般化:ポリゴンオフセットは自己シャドウイングのアーティファクトを避けるためにシャドウマップで使われます。現在のGPU上ではプリミティブについてポリゴンオフセットは定数です。対数ラスタライズ化に関しては,ある方向において線形的に変化するオフセットを必要とします。これは,各ピクセルにおいて深度を計算するために使用される方程式の定数を小さく変化さえることで実装可能です。
- ●新しい深度圧縮スキーム:深度圧縮はメモリ帯域幅の要件を減らすために重要です。プリミティブの平面性を活用する既存の深度圧縮技法は対数ラスタライズ化で平面が湾曲するためパフォーマンスが低下します。我々が提案する深度圧縮スキームは対数ラスタライズ化についてよく合致します。実際には,線形ラスタライズ化についてもうまく動作します。
これらの拡張は現在のGPU上で線形ラスタライズ化に匹敵するフィルレートで対数ラスタライズ化を有効にします。従って,LogPSMsは既存のアルゴリズムに基づく上に既存のアルゴリズムと同様のパフォーマンス特性を持つ必要があります。
1.8 Thesis organization
Chapter2では,シャドウマップアルゴリズムの最新法をレビューします。様々な種類のシャドウマップアーティファクトとそれらを取り扱うために提案された手法を議論します。また,代替となるシャドウ生成アルゴリズムも議論します。Chapter3は2次元と3次元の両方である点におけるエイリアシング誤差を定量化するための式を紹介します。Chapter4では,適切なパラメータライゼーションを計算することによって最小限のシャドウマップ解像度を用いてエイリアシング誤差を最小化する方法について議論します。導出されたパラメータライゼーションは実際に使用するためには適していませんが,単純なパラメータライゼーションを評価するためのベースラインとしては機能します。また,視錐台全体とすべてのライト方向上の一般誤差測定基準も議論します。Chapter5は様々なワーピングとパーティショニングスキームとそれらの組み合わせの解析を含みます。異なるワーピングパラメータ値,視錐台パラメータ,そしてライト位置についてそれらのアルゴリズムの振る舞いを調査します。LogPSMパラメータライゼーションと実験によって立証できる結果の詳細を示します。さらに,既存のアルゴリズムに対していくつかの改善を提案します。Chapter6では,既存のシャドウマップアルゴリズムとLopPSMsのさまざまな実装詳細について議論します。Chapter7は対数ラスタライズ化をサポートするために必要とされるハードウェア拡張を記述します。最後に,Chapter8で要点と今後の展望について示し結論付けます。
<編集注>
※アイサンプル:カメラ方向から見たときのサンプルのこと
※ライトサンプル:ライト方向から見たときのサンプルのこと