Eric Heiz, Jonathan Dupuy, Stephen Hill, David Neubeltらによる”Real-Time Polygonal-Light Shading with Linearly Transformed Cosines”の読みたいところだけを訳していこうかと思います。いつもながら誤字・誤訳が多々あると思いますので,ご指摘いただける場合は正しい翻訳例とともに指摘をしていただけるとありがたいです。
3 Linearly Transformed Spherical Distributions
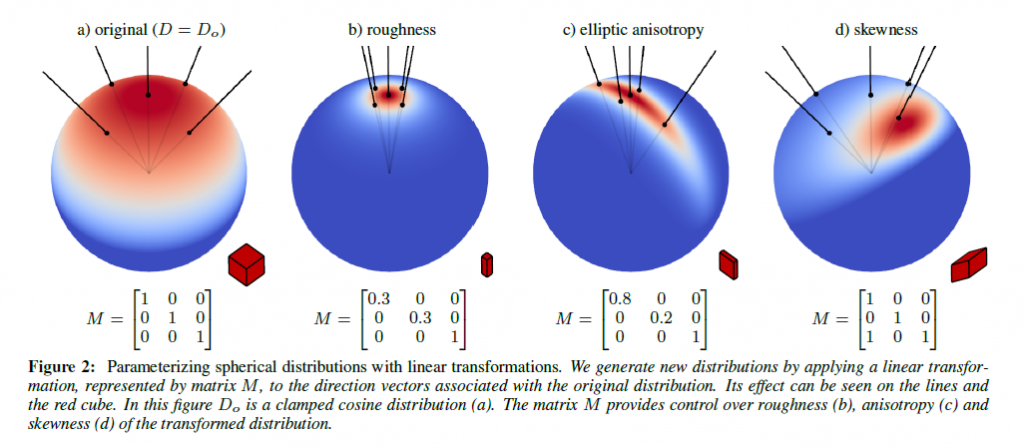
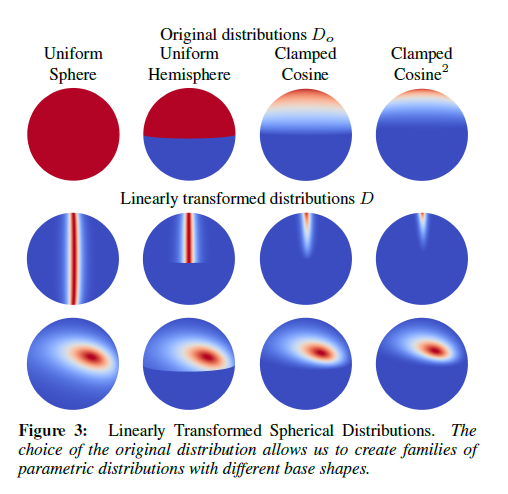
このセクションでは,線形変換した球面分布(LTSDs)を紹介します。方向ベクトルに対する線形変換を適用することによってもとの分布が形状を変える方法を示し(図2),この方法で新しい分布を定義し(図3),それらの性質について説明します。
“Real-Time Polygonal-Light Shading with Linearly Transformed Cosines”,
SIGGRAPH 2016, https://blogs.unity3d.com/jp/2016/05/26/real-time-polygonal-light-shading-with-linearly-transformed-cosines/ より引用
“Real-Time Polygonal-Light Shading with Linearly Transformed Cosines”,
SIGGRAPH 2016, https://blogs.unity3d.com/jp/2016/05/26/real-time-polygonal-light-shading-with-linearly-transformed-cosines/ より引用
3.1 Definition
Original Distribution to be Transformed
\(D_o\)は線形変換で再パラメータ化されるもとの分布を示します。図3で示したように,\(D_o\)の選択は変換される基本形状の制御をします。
Linear Transformations
新しい分布\(D\)を生成するために,元の分布\(D_o\)の方向ベクトル\(\omega_o\)に対して3×3行列\(M\)によってあらわされる線形変換を適用します。図2は\(M\)の選択が分布の性質にどのような影響を与えるかを示しています。論文を通して注意してほしいのは,正規化された方向ベクトルを想定しているということです。つまり,正確な変換は\(\omega = M \omega_o / || M \omega_o ||\)で,逆変換:\(\omega_o = M^{-1} \omega / || M^{-1} \omega ||\)を持つ元々の方向を相互にカバーします。
Closed-Form Expression
LTSDの大きさは,球面変換の分布のために評価された立体角の変化によって乗算された元の方向\(\omega_o\)上の元々の分布\(D_o\)の大きさで,次の閉形式を持ちます:
\begin{eqnarray}
D(\omega) = D_o(\omega_o)\frac{\partial \omega_o}{\partial \omega} = D_o \left( \frac{M^{-1}\omega}{|| M^{-1} \omega ||} \right) \frac{|M^{-1}|}{|| M^{-1}\omega||^3}, \tag{1}
\end{eqnarray}
ここで,\(\frac{\partial \omega_o}{\partial \omega} = \frac{|M^{-1}|}{||M^{-1} \omega||^3}\)は正規化されたベクトル\(\omega = M \omega_o / || M\omega_o||\)のヤコビアンです。この結果の証明はAppendix Aに載せています。
Shape Invariance
スケーリングベクトルはその方向を変化させないので,スケーリング変換(\(M = \lambda I\))による分布は変わりません。さらに,回転は分布の向きのみを変化させ,形状は変えません。これはなぜかというと\(M\)がスケーリングまたは回転行列の場合に球面変換のヤコビアンが定数:\(\frac{\partial \omega_o}{\partial \omega} = 1\)となるからです。
Median Vector
幾つかの古典的な分布\(D_o\)では,z軸のベクトル(\(0 \, 0 \, 1)^T\)が中間ベクトルです。すなわち,このベクトルを含む任意の平面を重みが\(\frac{1}{2}\)に等しくなる2つの部分へと分けます。この性質は変換によって保たれます:変換された中間ベクトルは変換された分布\(D\)の中間ベクトルとなります。図2の構成すべてにおいて,\(M\)の右列は\((0 \, 0 \, 1)^T\)となります。つまり,中間ベクトルはz軸に沿って保たれたままです。例として,図2.dにおいて,歪みは分布をある側に押しつぶし,もう一方を引き延ばし,z軸は分布の中間に保たれます。
3.2 Properties
変換された分布\(D\)は元の分布\(D_o\)のいくつかの性質を継承します。
Normalization
LTSD \(D\)のノルムは,元の分布\(D_o\)のノルムとなります。式(1)を使って次を得ます。
\begin{eqnarray}
\int_{\Omega} D(\omega) d\omega = \int_{\Omega} D_o (\omega_o) \frac{\partial \omega_o}{\partial \omega} d\omega = \int_{\Omega} D_o(\omega_o) d\omega_o. \tag{2}
\end{eqnarray}
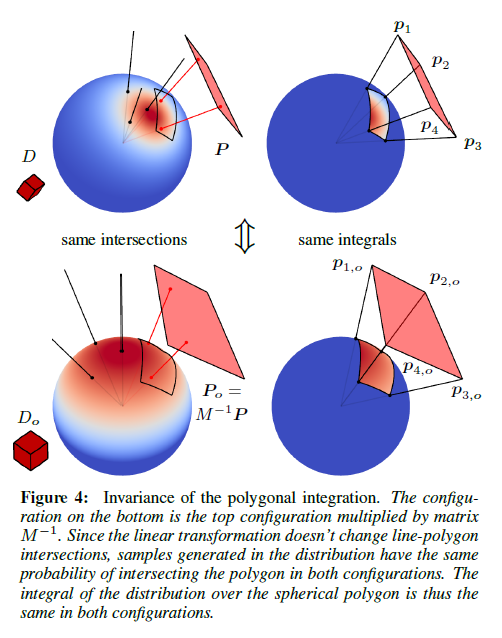
Integration over Polygons
ポリゴン\(P\)についてのLTSD \(D\)の積分はポリゴンの各頂点に対して逆変換\(M^{-1}\)を適用することによって得られるポリゴン\(P_o = M^{-1}P\)について元の分布\(D_o\)の積分となります:
\begin{eqnarray}
\int_P D(\omega) d\omega = \int_{P_o} D_o(\omega_o)d\omega, \tag{3}
\end{eqnarray}
式(2)として同じ変化の変数で得られます。この結果の説明を図4に示します。直感的には,式(3)における積分はポリゴン\(P\)で交差する\(D\)上で直接サンプルされる可能性があります。任意の線形変換は\(D\)の方向ベクトルとこの交差で変化しないポリゴン\(P\)の両方に適用され,したがって積分の値は保たれます。あるポリゴンをその他のポリゴン\(P_o = M^{-1}P\)へと,そして分布\(D\)を元の分布\(D_o\)に変換する\(M^{-1}\)を適用することによってこの性質を使用します。結果として,\(D\)の\(P\)についての積分は\(D_o\)の\(P_o\)についての積分と等しくなります。
“Real-Time Polygonal-Light Shading with Linearly Transformed Cosines”,
SIGGRAPH 2016, https://blogs.unity3d.com/jp/2016/05/26/real-time-polygonal-light-shading-with-linearly-transformed-cosines/ より引用
Importance Sampling
LTSDsの定義のおかげて,\(D\)になる可能性がある場合に\(D_o\)は重点サンプルすることができます。アルゴリズム1で示すように,\(D_o\)からランダムサンプル\(\omega_o\)を生成し,\(\omega = \frac{M \omega_o}{||M \omega_o||}\)を
変換します。式(1)におけるLTSDの定義は\(D_o\)はこの変換のヤコビアンによって乗算され,サンプル\(\omega\)の確率密度関数(PDF)は正確に\(D(\omega)\)となります。

“Real-Time Polygonal-Light Shading with Linearly Transformed Cosines”,
SIGGRAPH 2016, https://blogs.unity3d.com/jp/2016/05/26/real-time-polygonal-light-shading-with-linearly-transformed-cosines/ より引用
4 Approximating Physically Based BRDFs with Linearly Transformed Cosines
このセクションでは,物理ベースBRDFの良い近似を生み出す線形変換された分布のファミリーを生成するのを可能にする元の分布についてクランプされたコサイン分布を選択する方法を示します。
Linearly Transformed Cosines
元の分布\(D_o\)について,\(z\)方向によって与えられた半球上のクランプされた正規化コサイン分布を選択します:
\begin{eqnarray}
D_o (\omega_o = (x, y, z)) = \frac{1}{\pi} \max (0, z), \tag{4}
\end{eqnarray}
そして,線形変換されたコサイン(LTCs)は式(1)において\(D_o\)を置換することによって定義されます。
Fitting
我々はGGXマイクロファセットBRDF[Walter et al. 2007]の近似を選択します。そのBRDFは現在,最もリアリスティックなパラメトリックなBRDF[Hill et al. 2015]とされています。より具体的には,ライト方向\(\omega_l\)についてコサインで重みづけされたBRDFによって与えられる球面関数を近似します:
\begin{eqnarray}
D \approx \rho(\omega_v, \omega_l) \cos \theta_l. \tag{5}
\end{eqnarray}
等方性マテリアルについて,BRDFは入射方向\(\omega_v = (\sin\theta_v, 0, \cos\theta_v)\)とラフネスパラメータ\(\alpha\)に依存します。任意の組み合わせ\((\theta_v, \alpha)\)について,線形変換されたコサインで重みづけされたBRDFをフィットします。すなわち最も良いフィットを生み出す行列\(M\)を求めます。等方性BRDFの平面の対称性と線形変換されたコサインがスケールに不変であるため,\(M\)は次のように表されます
\begin{eqnarray}
M = \begin{bmatrix} a & 0 & b \\ 0 & c & 0 \\ d & 0 & 1 \end{bmatrix}, \tag{6}
\end{eqnarray}
このため,フィットが必要となるパラメータは4つのみです。経験的に,\(L^3\)誤差を最小化することがシェーディングにおいて最も良いビジュアルの結果を生み出すということがわかりました。図5はフィッティング結果を示します。

“Real-Time Polygonal-Light Shading with Linearly Transformed Cosines”,
SIGGRAPH 2016, https://blogs.unity3d.com/jp/2016/05/26/real-time-polygonal-light-shading-with-linearly-transformed-cosines/ より引用
Representation and Storage
式(3)におけるポリゴンの積分は逆行列\(M^{-1}\)のみを必要とします。フィッティング後の手順で,我々は事前計算されたテーブル上で逆行列を保存します。式(6)と同様に,\(M^{-1}\)は等方性BRDFについて4パラメータによってあらわすことが可能です。さらに,フィットされたBRDFのノルム\(\int_{\Omega} \rho(\omega_v, \omega_l)\cos\theta_l d \omega_l\)について追加のパラメータを使用します。我々は合計5つのパラメータを64×64の解像度で,\(\theta \in [0, \frac{\pi}{2}]\)と\(\sqrt{\alpha} \in [0, 1]\)によってパラメータ化された2次元浮動小数テクスチャ上に保存し,線形補間でフェッチされます。事前計算データのサイズは80KBです。
5 Real-Time Polygonal-Light Shading with Linearly Transformed Cosines
ディフューズのポリゴンのライトでシェーディングすることはポリゴン領域についての照明積分を計算することを意味します:
\begin{eqnarray}
I = \int_P L(\omega_l)\rho(\omega_v, \omega_l) \cos \theta_l d \omega_l, \tag{7}
\end{eqnarray}
ここで,\(\omega_v\)は視線方向で,\(\rho\)はBRDF,\(P\)はポリゴン,そして方向\(\omega_l\)から受け取ったポリゴンによって放たれる放射輝度\(L\)です。ランタイムで線形変換されたコサインの性質を使用するために,入射各\(\theta_v\)と,BRDFのラフネス\(\alpha\)に関係する線形変換されたコサイン\(D\)の行列\(M^{-1}\)をフェッチし,式(7)における式(5)の近似を使用します:
\begin{eqnarray}
I &=& \int_P L(\omega_l) \rho(\omega_v, \omega_l) \cos \theta_l d \omega_l \\
& \approx & \int_P L(\omega_l)D(\omega_l) d \omega_l. \tag{8}
\end{eqnarray}
5.1 Shading with Constant Polygon Lights
ポリゴンライトによって放たれた放射輝度が空間的に一定である場合,つまり,\(L(\omega_l) = L\)の場合,積分の分離可能な乗算因子となります
\begin{eqnarray}
I = \int_P L(\omega_l)D(\omega_l)d\omega_l = L \int_P D(\omega_l)d\omega_l. \tag{9}
\end{eqnarray}
式(3)からのポリゴンの積分の性質のため,次のように簡略できます
\begin{eqnarray}
\int_P D(\omega) d\omega = \int_{P_o} D_o(\omega_o)d\omega_o = E(P_o), \tag{10}
\end{eqnarray}
ここで,\(E\)はポリゴン\(P_o = M^{-1}P\)の放射照度です。確かに\(D_o\)はクランプされたコサイン分布であるので,ポリゴンについての積分はこのポリゴンの放射照度となり,閉形式を持ちます[Baumら 1989]:
\begin{eqnarray}
E(p_1, …, p_n) = \frac{1}{2 \pi} \sum_{i=1}^{n} {\rm{acos}} (\langle p_i, p_j \rangle) \langle \frac{pi \times p_j}{|| p_i \times p_j ||}, \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \rangle, \tag{11}
\end{eqnarray}
そして,\(j = (i + 1) {\rm{mod}} n\)となります。式は半球の上側に位置する球面ポリゴンを想定していることに注意してください。実際には,式(11)の総和のにおける寄与を加算するためにポリゴンの各エッジをクリップします。
5.2 Shading with Textured Polygonal Lights
このセクションでは,ポリゴンによって放たれる放射輝度\(L(\omega_l)\)は2次元のカラーテクスチャを適用することによって表されます。この場合においては,積分から分離することができません。式(8)を次のように書き直します:
\begin{eqnarray}
I & \approx & \int_P L(\omega_l)D(\omega_l)d\omega_l = I_D I_L, \tag{12} \\
I_D &=& \int_P D(\omega_l)d\omega_l, \tag{13} \\
I_L &=& \frac{\int_P L(\omega_l) D(\omega_l) d\omega_l}{\int_P D(\omega_l) d\omega_l}. \tag{14}
\end{eqnarray}
この式の利点は,\(I_D\)と\(I_L\)を計算するという異なる性質の2つの部分問題へと分けることが可能なことです。
The Shape of the Highlight
\(I_D\)の値はポリゴン領域についての分布の積分となります。すなわち,\(P\)と交差する\(D\)におけるレイの比となります。その導出は積分\(I\)のオーダーの大きさとハイライトを形作ります。我々は式(3)で正確な値を計算します。
The Color of the Highlight
対照的に,\(I_L\)は\(P\)と交差する\(D\)におけるレイによって集められる平均的な色と見ることができ,ハイライトの色について重要となります。テクスチャ空間のフィルタとして定式化することができ,我々は事前フィルタされたテクスチャで近似することを提案します。以下で,我々は詳細度レベル(LODs)を持つテクスチャの事前フィルタの方法と,テクスチャフェッチのパラメータ化を説明します。
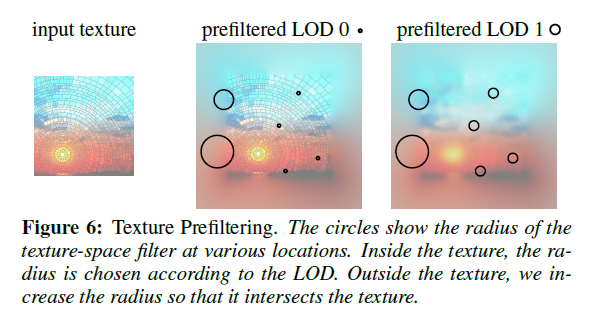
5.3 Texture Prefiltering
式(14)はテクスチャ空間に射影された\(F(\omega_l) = \frac{D(\omega_l)}{\int_P D(\omega_l)d\omega_l}\)のフィルタを通じてテクスチャの値として渡された\(L\)を定義します。事前フィルタステップにおいて,テクスチャ空間のガウスフィルタで\(F\)を近似します。近似フィルタによって保存される(F\)の性質は2つあります:\(F\)はポリゴンへとクランプされます。すなわち,テクスチャの外側は\(F=0\)となり,テクスチャ内へと\(F\)は正規化されます:\(\int_P F(\omega_)d\omega_l = 1\)。実際には,テクスチャ空間フィルタはテクスチャの外側へと漏れ出すことができないように近似することを意味します。これを達成するために,我々はテクスチャ内へとテクスチャ空間ガウシアンをクランプし再正規化します。図6に図示されるように,我々はテクスチャ周りのマージンを導入します。この領域において,テクスチャと交差するためにフィルタの半径を増加させます。これはフィルタを明確に定義するために必要です。最終的に,マージンを超える,エッジへとテクスチャ座標をクランプします。これはテクスチャの外側のテクスチャ空間のどこでも低周波の関数でスムースな定義を表します。それは正確なフィルタ\(F\)から予測されます。
“Real-Time Polygonal-Light Shading with Linearly Transformed Cosines”,
SIGGRAPH 2016, https://blogs.unity3d.com/jp/2016/05/26/real-time-polygonal-light-shading-with-linearly-transformed-cosines/ より引用
5.4 Texture Fetching
On the Difficulty of Fetching Prefiltered Area-Light Textures
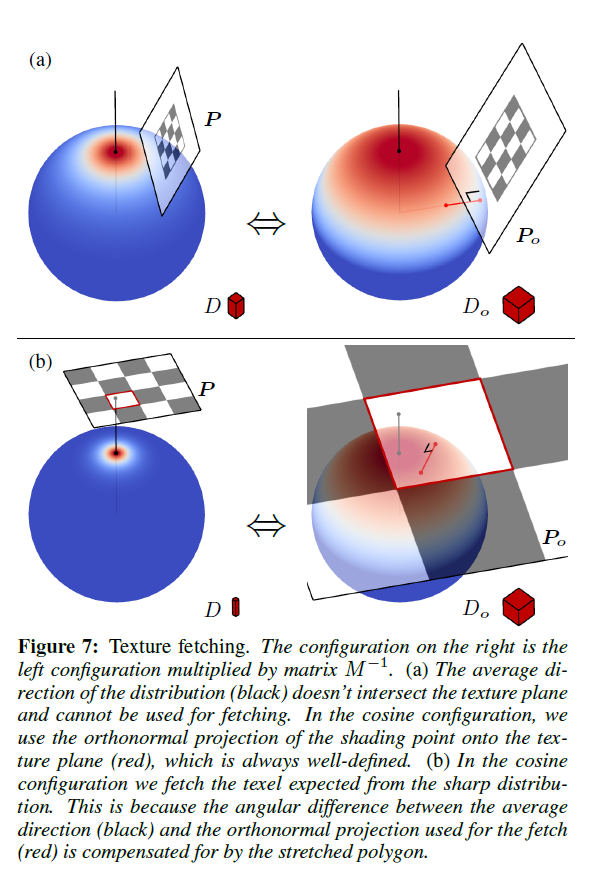
テクスチャフェッチをパラメータ化するには、テクスチャ座標とLODの2つが必要です。 素朴なアプローチは、分布の平均(または中央値)方向の交点のテクスチャ空間における座標を計算することから成り立ちます。 このアプローチは不安定であり、時には不確定です。 例えば、図7aでは、分布の平均方向がテクスチャ平面と交差しません。 別の問題は、適切なLODがいくつかのパラメータに依存することです:分布の鮮明度、およびテクスチャ平面の傾きおよび距離に依存します。
Simplifying the Problem with the Cosine Configuration
問題を簡単にするために,\(D\)と関連するコサイン形状で表現します。この変換は図7で図示されます。式(3)におけるポリゴンの積分について,我々は設定のために逆行列\(M^{-1}\)を適用します。すなわち
\begin{eqnarray}
I_L = \frac{\int_P L(\omega_l) D(\omega_l)d\omega_l}{\int_P D(\omega_l) d\omega_l} = \frac{\int_{P_o} L_o(\omega_l)D_o(\omega_l)d\omega_l}{\int_{P_o}D_o(\omega_l)d\omega_l}, \tag{15}
\end{eqnarray}
ここで,\(P_o = M^{-1}P\)はコサイン形状におけるポリゴンで,\(L_o(\omega_l)\)は関係する変換されたテクスチャです。この形状の利点はより簡単に,任意の分布\(D\)に対してより頑健にコサイン分布\(D_o\)を近似するテクスチャ空間フィルタをパラメータ化することです。
Fetching the Perfiltered Texture in the Consine Configuration
コサイン形状において,我々はテクスチャ平面へのシェーディング点の正射影を使用します(図7)。この点は常に明確に定義され,計算するのが簡単で,図7.bに示すように分布\(D\)の鮮明さに関係なく正確なテクスチャフェッチを生み出します。さらに,正射影のため,この点にテクスチャ平面の傾きは正確に90度であり,それゆえテクスチャ空間フィルタ形状に対して違方性を導入しません。ポリゴンの変形後のコサイン分布の低周波変動とテクスチャパラメータ化の異方性歪みは無視します。LODの選択は、テクスチャ平面に対する二乗距離\(r^2\)とポリゴンの面積\(A\)との比の1次元関数へと減らします。我々はテクスチャ空間におけるガウシアンの標準偏差\(\sigma = \sqrt{\frac{r^2}{2A}}\)で事前フィルタされたLODを選択します。
“Real-Time Polygonal-Light Shading with Linearly Transformed Cosines”,
SIGGRAPH 2016, https://blogs.unity3d.com/jp/2016/05/26/real-time-polygonal-light-shading-with-linearly-transformed-cosines/ より引用
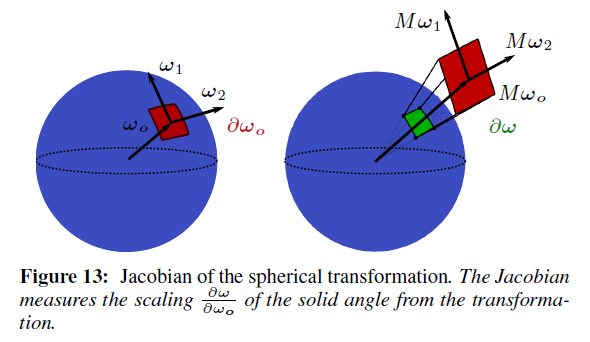
A Derivation of the Jacobian
式(1)のヤコビアンを導出します。球面変換のヤコビアンは図13において図示される立体角の変化を測ります。正規直交規定\((\omega_o, \omega_1, \omega_2)\)を持つオリジナル形状と赤色の領域で表される微小立体角\(\partial \omega_o\)から始めます。行列\(M\)によって乗算することによって形状を変換します。新しい微小立体角は緑色の領域によってあらわされる\(\partial \omega\)で計測されます。球の表面は変換された微小平面の射影によって覆われます。
“Real-Time Polygonal-Light Shading with Linearly Transformed Cosines”,
SIGGRAPH 2016, https://blogs.unity3d.com/jp/2016/05/26/real-time-polygonal-light-shading-with-linearly-transformed-cosines/ より引用
図14は新しい立体角\(\partial \omega\)を計算する方法を示しています。それは次によって与えられます
\begin{eqnarray}
\partial \omega = \partial \omega_o A \frac{\cos \theta}{r^2}, \tag{16}
\end{eqnarray}
ここで,\(\partial \omega_o A\)は変換後の立体角(あるいはサーフェイスエレメント)で,\(r\)は球の中心への距離で,\(\theta\)はその方向と法線間の角度の差分です。

“Real-Time Polygonal-Light Shading with Linearly Transformed Cosines”,
SIGGRAPH 2016, https://blogs.unity3d.com/jp/2016/05/26/real-time-polygonal-light-shading-with-linearly-transformed-cosines/ より引用
展開し,式(16)で簡略化し,線形代数の性質を使用します。
\begin{eqnarray}
M\omega_1 \times M \omega_2 &=& |M| M^{-T}(\omega_1 \times \omega_2) \\
&=& |M| M^{-T}\omega_o, \tag{17}
\end{eqnarray}
そして,整理後に次を得ます
\begin{eqnarray}
\frac{\partial \omega}{\partial \omega_o} = \frac{|M|}{||M \omega_o||^3}, \tag{18}
\end{eqnarray}
そして逆数は,
\begin{eqnarray}
\frac{\partial \omega_o}{\partial \omega} = \frac{|M^{-1}|}{||M^{-1}\omega||^3}, \tag{19}
\end{eqnarray}
です。
上式は式(1)で使用されるヤコビアンです。