D. Brandon Lloyd氏の博士論文である，Logarithmic Perspective Shadow Mapsを適当に訳していくことにします。
前回はChapter.4を何とか訳しました。今回はいよいよメインであるシャドウマップアルゴリズムの解析になるChapter.5を訳していきます。
誤訳があったりなど，日本語としては多々見苦しい点があるかと思いますが，そこはご容赦ください。

---

CHAPTER 5

Analysis of shadow map algorithm

この章では，4章で開発した誤差尺度を用いていくつかのシャドウマップアルゴリズムを解析します。この章は主に3つの部分から構成されます。第1に，視錐台の面のパラメータライゼーションを解析します。第2に，視錐台全体のパラメータライゼーションをするためにこの解析を拡張します。第3に，いくつかのアルゴリズムを比較します。我々は4つの異なるパラメータライゼーションを考えます。

• ●Uniform. 標準シャドウマップによって使用されます。
• ●Perspective. 既存のワーピング手法によって使用されます。
• ●Logarithmic. 透視パラメータライゼーションについて改善するものとして何人かの研究者によって提案されたパラメータライゼーション。
• ●Logarichmic＋perspective. LogPSMsの基礎となるパラメータライゼーション。

これらのパラメータライゼーションの振る舞い全般を最大誤差と同じように考察します。対数+透視 パラメータライゼーションが透視エイリアシング上で，タイトな領域から導かれる最適に近いパラメータライゼーションによって生成されるのと同じオーダとなる最悪の場合に，最大誤差を生成することを示します（式4.42-4.44）。面に対して\(z\)分割を適用することの効果も観察し，面分割で起因するシアリングアーティファクトを解決するのを試みます。また，我々は新しい\(z\)-パーティショニングスキームも提案します。
　フェイスパラメータライゼーションの分析をより複雑な錐台全体をパラメータライズする場合へと拡張します。錐台パラメータライゼーションはライトの方向が視線方向に近づくにつれてユニフォームパラメタライゼーションに収束しなければなりません。ワーピングパラメータを選択するために改善されたアルゴリズムを定式化するためにライト方向の範囲上の誤差を解析します。
　様々なアルゴリズムを比較することによってこの章を結びます。我々は実験結果と，対数透視パラメータライゼーションが利用できない時に低誤差のシャドウマップを得るための方法を追加的な分析を示します。
 

5.1 Face parameterization

4章では，\(\delta_b\) が面に依存，そして我々が考察する面に沿った方向に依存する3つの異なる形式を持つことを見てきました(式4.20, 4.26そして4.28)。ライト画像平面上の位置の関数として任意のパラメータライゼーションに対する錐台の面上の透視エイリアシング誤差領域が式4.4へとこれらの式を代入することによって計算することが可能です：

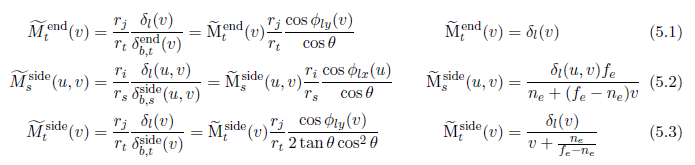
\(\tilde{\rm M}\) を透視エイリアシング誤差の基本分布と名付けます。透視，対数，そして対数透視パラメータライゼーションに対してこれらのパラメータライゼーションは側面のみに適用されるので上付き文字をつけます。解像度と \(\theta\) の項は透視エイリアシング誤差の全体スケールに影響を及ぼします。ディレクショナルライトに対して，\(\cos{\phi_l}\) の項は定数で，従ってスケール全体にのみ影響しますが，ポイントライトに対しては \(\cos{\phi_l}\) は基本誤差分布を調節します。図5.1は，面上の変化する高さにおいてライトに対する \(\cos{\phi_l}\) の項を示しています。基本誤差分布を分離することで，解析のいくつかを簡素化します。また，簡素化することで これらの項が\(\tilde{\rm M}\) のみを含むだけになるので，\(n_e\) と \(f_e\) 上の誤差の依存を簡単に見ることができるようになります。また，\(\tilde{\rm M}\) の項で基本重要解像度 \(\rm R\) と基本ストレージ要因 \(\rm S\) も定義します：
\begin{eqnarray}
{\rm R} &=& \max_v \left( \tilde{\rm M} (v) \right) \tag{5.4} \\
{\rm S} &=& {\rm R}_s{\rm R}_t \tag{5.5}
\end{eqnarray}
この論文中で使われる様々な誤差尺度の概要は表5.1に記載されます。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.72 より引用。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.72 より引用。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.72 より引用。

 

5.1.1 Uniform parmaterization.

シャドウマップパラメータライゼーションはライト画像平面上の\(u\) と \(v\) の関数としてシャドウマップ上の \(s\) と \(t\) の座標についての関数として構成されます。最も単純なシャドウマップパラメータライゼーションは以下です：
\begin{eqnarray}
{\bf F}_{un}(u, v) &=& \begin{bmatrix} s(u,v) \\ t(v) \end{bmatrix} = \begin{bmatrix} u \\ v \end{bmatrix} \tag{5.6} \\
\delta_{un} &=& 1 \tag{5.7}
\end{eqnarray}
ユニフォームパラメータライゼーションに対する重要解像度因子は式4.5から計算することが可能です。例として側面上では次を得ます：
\begin{eqnarray}
R_{un,s}^{\rm side} &=& \max \left( \tilde{M}_{un, s}^{\rm side}(u, v) \right) = \max \left( \tilde{\rm M}_{un, s}^{\rm side}(u, v) \frac{\cos\phi_{lx}(u)}{\cos\theta} \right) \tag{5.8} \\
\tilde{\rm M}_{un,s}^{\rm side} &=& \frac{f_e}{n_e + (f_e – n_e)v} \tag{5.9}
\end{eqnarray}
図5.2は変化するライト位置に対する \({\sf R}_{un}^{\rm side}\) と \({\sf R}_{un}^{\rm side}\) を示しています。ライト位置が面上にあるときに各 \(R_{un}\) が最大値に達するということに注意してください。これはなぜかというと \(\cos\phi_{ly}\) の要素が \(y(v) = l_y\) である点に対して最大値に達するためです。図5.2と図4.8を比較すると，ライトが直接面上にないときに，グラフの形状はほぼ同一ですが，側面上では，\(\tilde{\rm M}_{un,s}^{\rm side}\) と \(\tilde{\rm M}_{un,t}^{\rm side}\) が面上で \(f_e/n_e\) の最大値を持つためプロットの大きさが著しく異なります。

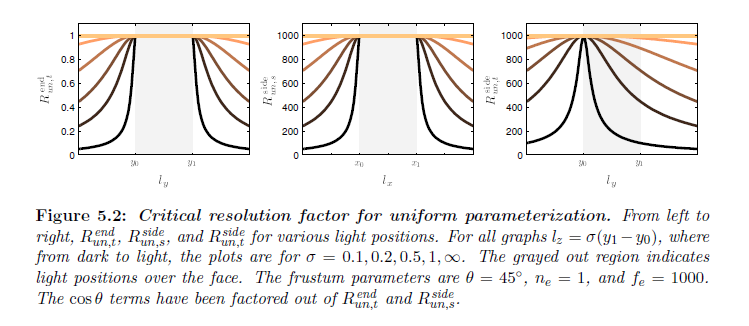
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.74 より引用。

 

5.1.1.1 Maximum error

4.4節では，視錐台上のすべての点についてと画像として同じ解像度を持つシャドウマップを用いた全てのライトの方向についての最大透視エイリアシング誤差である誤差尺度 \(\sf R\) を導入しました。\({\sf R}_{un}\) は \(R_{un}\) において，\(\cos\phi_l = 1\) を設定することによって計算できる可能性があります。これにより \({\sf R}_{un,t}^{\rm end}\) が一定になります。\({\sf R}_{un,s}^{\rm side}\) と \({\sf R}_{un,t}^{\rm side}\) について，\(\tilde{\rm M}_{un,s}^{\rm side}\) と \(\tilde{\rm M}_{un,t}^{\rm side}\) の項は \(v=0\) において最大値を持ちます。従って，ユニフォームパラメータライゼーションを持つ最大誤差について次を得ます：
\begin{eqnarray}
{\sf R}_{un,t}^{\rm end} &=& \frac{1}{\cos\theta} \tag{5.10} \\
{\sf R}_{un,s}^{\rm side} &=& \frac{f_e}{n_e\cos\theta} \tag{5.11} \\
{\sf R}_{un,t}^{\rm side} &=& \frac{f_e – n_e}{2n_e\tan\theta\cos^2\theta} \tag{5.12} \\
{\sf S}_{un}^{\rm side} &=& {\sf R}_{un,s}^{\rm side}{\sf R}_{un,t}^{\rm side} = (f_e/n_e) \frac{\left( (f_e / n_e) – 1 \right)}{2\tan\theta\cos^3\theta} \tag{5.13}
\end{eqnarray}
ユニフォームパラメタライゼーションに対する重要解像度は \(F_b^{\rm end}\) のものと等しくなります。側面について，各方向における最大誤差は \(O(f_e/n_e)\)で，さらに両方の方向を組み合わせた誤差は \(O((f_e/n_e)^2)\) です。
 

5.1.2 Perspective parameterization.

透視パラメータライゼーションは図5.3に示すような側面の周囲に台形のワーピング錐台に配置します。パラメータライゼーションは正方形のシャドウマップへとワーピング錐台をマップします。ワーピングの強さはワーピング錐台のニア平面までの距離 \(n’\) によって制御されます。

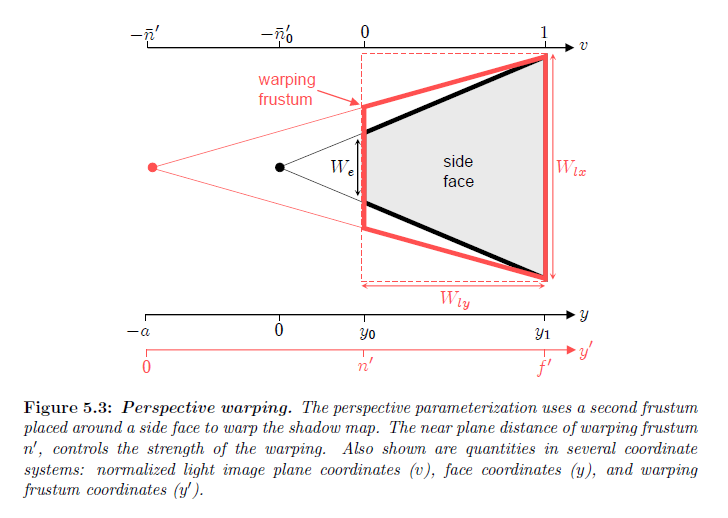
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.75 より引用。

　図5.3は透視パラメータライゼーションを解析するために使われる3つの異なる座標のセットを示しています。正規化されたライト平面座標 \((v)\) は視錐台の全体のスケールに非依存であるため使い勝手が良いです。\({\bar n}’\) は正規化されたワーピングパラメータです。\({\bar n}’_0\) はカメラから見たときの正規化された位置座標です。4章で導入された面座標系 \((y)\) は指定した面に相対な位置について最もあっています。面座標系の起点はカメラの位置においてになります。ワーピングした錐台座標 \((y’)\) は面座標系と起点が距離 \(a = n’ -y_0\) によって \(y\) に沿ってシフトバックされるということを除いて同じになります。ワーピングした錐台座標は以下の単純な関係を用いて正規化された座標系における量によって表現することができます：
\begin{eqnarray}
y’ &=& W_{ly}(v + {\bar n}’) \tag{5.14} \\
n’ &=& W_{ly}{\bar n}’ \tag{5.15} \\
f’ &=& W_{ly}({\bar n}’ + 1) \tag{5.16}
\end{eqnarray}
透視パラメタライゼーションは2次元の射影行列を用いてワーピング錐台座標上で最もうまく明記されます：
\begin{eqnarray}
{\bf F}_p &=& \begin{bmatrix} s \\ t \end{bmatrix} = \begin{bmatrix} x’_p / w’_p \\ y’_p / w’_p \end{bmatrix} \tag{5.19} \\
\begin{bmatrix} x’_p \\ y’_p \\ w’_p \end{bmatrix} &=& \begin{bmatrix} p_0 & p_1 & 0 \\ 0 & p_2 & p_3 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x’ \\ y’ \\ 1 \end{bmatrix} \tag{5.20}
\end{eqnarray}
\begin{eqnarray}
p_0 &=& \frac{f’}{W_{lx}} \\
p_1 &=& \frac{1}{2} \\
p_2 &=& \frac{f’}{f’ – n’} \\
p_3 &=& -p_2n’ \tag{5.21}
\end{eqnarray}
\({\bf F}_p\) によって生成される間隔分布関数を得るために，\(F_{p,s}\) ， \(F_{p,s}\) ，\(x’\) と \(y’\) そして \(1/W_{lx}\) と \(1/W_{ly}\) によってスケールされたそれぞれについての派生物の逆数をとります：
\begin{eqnarray}
\delta_{p,s} &=& \frac{y’}{f’} &=& \frac{v+{\bar n}’}{{\bar n}’ + 1} \tag{5.22} \\
\delta_{p,t} &=& \frac{(y’)^2}{n’f’} &=& \frac{(v + {\bar n}’)^2}{{\bar n}’ ({\bar n}’ + 1)} \tag{5.23}
\end{eqnarray}
\(\delta_{p,s}\) は \(u\) 上で一定であり，\(v\) 上で線形に増加します。\(\delta_{p,t}\) は \(v\) 上で 2次となります。ライトサンプルの間隔は2次的に増加し，カメラのサンプル空間は線形に増加するので，透視パラメータライゼーションは透視エイリアシング誤差を取り除くことができません。しかしながら，面白いことに，単一平面について透視と射影エイリアシング誤差の合成は取り除くことが可能です(Chong & Gortler, 2004)。
\(\delta_b^{\rm side}\) の部分(式4.26 と 4.28) は \(n_e\) と \(f_e\) に依存しており，\({\bar n}’_0\) の項で書き直すことができます：
\begin{eqnarray}
\frac{n_e + (f_e – n_e) v}{f_e} = \frac{v + {\bar n}’_0}{{\bar n}’_0 + 1} \tag{5.24} \\
v + \frac{n_e}{f_e – n_e} = v + {\bar n}’_0 \tag{5.25} \\
{\bar n}’_0 = \frac{n_e}{f_e – n_e} \tag{5.26}
\end{eqnarray}
これは，透視パラメータライゼーションについて基本誤差分布を次のように書くことができます：
\begin{eqnarray}
{\tilde {\rm M}}_{p,s} &=& \frac{(v + {\bar n}’)({\bar n}’_0 + 1)}{(v + {\bar n}’_0)({\bar n}’ + 1)} \tag{5.27} \\
{\tilde {\rm M}}_{p,t} &=& \frac{(v + {\bar n}’)^2}{{\bar n}'({\bar n}’ + 1)(v + {\bar n}’_0)} \tag{5.28}
\end{eqnarray}
図5.4は \({\bar n}’\) のいくつかの値についての \({\tilde {\rm M}}_{p,s}\) と \({\tilde {\rm M}}_{p,t}\) を示しています。\({\bar n}’ = {\bar n}’_0\) における \(s\) 上の誤差は均一で最小です。一方で，\(t\) 上の誤差は線形に増加します。このパラメータ値は頭上のディレクショナルライトに対してPSMで使われたものと一致します。\({\bar n}’ = {\bar n}’_{\rm LiSPSM}\) において，\(t\) 上の最大誤差は最小されますが，\(s\) 上における誤差は大きくなります。\({\bar n}’_{\rm LiSPSM}\) はLiSPSMで使われる正規化されたワーピングパラメータです(Wimmerら, 2004)：
\[
{\bar n}’_{\rm LiSPSM} = \frac{n_e + \sqrt{n_e f_e}}{f_e – n_e} \tag{5.29}
\]
\({\bar n}’ \rightarrow \infty\) につれて，透視パラメータライゼーションはユニフォームパラメータライゼーションへと収束します。最大誤差は \({\tilde {\rm M}}_{p,s}\) と \({\tilde {\rm M}}_{p,t}\) の両方について高くなります。

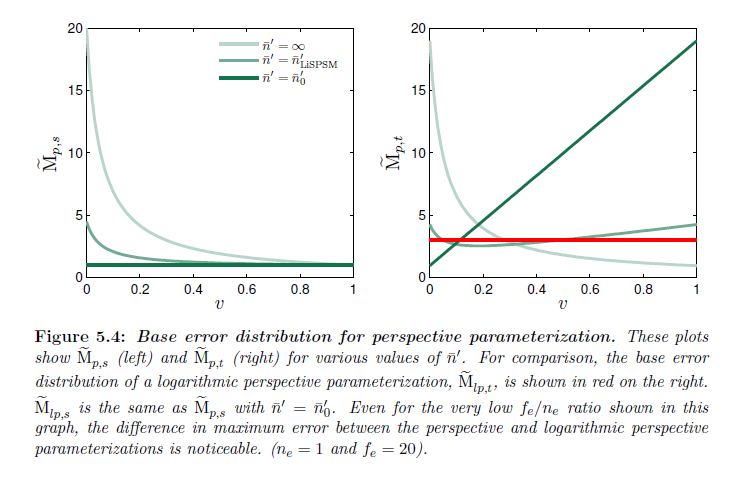
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.77 より引用。

 

5.1.2.1 Paramterizing the warping parameter

ワーピングパラメータ \({\bar n}’\) は直接的に動作させるためには適していません。\({\bar n}’ \in [{\bar n}’_0, \infty)\) の半無限範囲はグラフを書くのは難しいです。また，\({\bar n}’\) における変化と誤差における変化の相互関係は非線形であり，とても直感では理解できません。最大誤差 \({\rm R}\) の項において直接 \({\bar n}’\) をパラメータライズすることは便利であることが分かりました。
　最初のパラメータライゼーションは，\({\rm R}_{p,s} = \max \left({\tilde {\rm M}}_{p,s} \right)\) に基づきます。図5.4で見ることができように，この範囲では，\(v = 0\) において\({\tilde {\rm M}}_{p,s}\)の最大値が存在するので \({\bar n}’ \in [{\bar n}’_0, \infty]\) に対して \({\rm R}_{p,s} = {\tilde {\rm M}}_{p,s}(0)\) です。 \({\rm R}_{p,s}\) の値は \({\bar n}’ = \infty\) におけるその最大値（ワーピングなし）から，\({\bar n}’ = 0\) における最小値（ワーピング最大値）へと減少します。この観点に基づき，“ワーピングの量”として考えることができるパラメータ \(\omega \in [0,1]\) を定義します：
\begin{eqnarray}
\omega({\bar n}’) &=& \frac{{\rm R}_{p,s}({\bar n}) – {\rm R}_{p,s}({\bar n}’_0)}{{\rm R}_{p,s}(\infty) – {\rm R}_{p,s}({\bar n}’_0)} \\
&=& \frac{{\bar n}’_0 + 1}{({\bar n}’ + 1)} \tag{5.30} \\
{\bar n}'(\omega) &=& ({\bar n}’_0 + 1) \left( \frac{1}{\omega} – 1 \right) \tag{5.31}
\end{eqnarray}
ここで， \({\rm R}_{p,s}\) への引数はワーピングパラメータです。\(\omega\) が0から1へと線形に変化するにつれて，\({\bar n}’\) は(非線形に) \(\infty\) から \({\bar n}’_0\) へと下がる変化をし，ワーピングの強さは増加し，そして \({\rm R}_{p,s}\) の値はその最大値から最小値へと線形に変化します。ワーピング錐台のニア平面の幅もまた線形的に変化し \(W_{lx}\) から \(W_e\) へと下がります。従って，\(\omega\) もまた，ワーピング錐台の形状について直感的な制御となります。
　第2のパラメータライゼーションは，\({\rm R}_{p,t}\) に基づきます。ワーピングパラメータの範囲を超える\({\rm R}_{p,t}\) の振る舞いは \({\rm R}_{p,s}\) よりも若干複雑です。最大誤差は \({\bar n}’ \in [{\bar n}’_0, {\bar n}’_{\rm LiSPSM})\) についてファー平面(\(v=1\))においてと，\({\bar n}’ \in [{\bar n}’_{\rm LiSPSM}, \infty)\) についてニア平面(\(v=0\))において生じます。\(\omega\) を定義したのとほとんど同じように，パラメータ \(\eta \in [-1, 1]\) を定義します。ここで，\(\eta = -1\) はニア平面における最大誤差に一致し，\(\eta \in [-1, 0]\) の範囲上で最小値へと線形に減少します。そして，\(\eta \in [0,1]\) でファー平面上で再び同じ最大値へと線形に増加します：

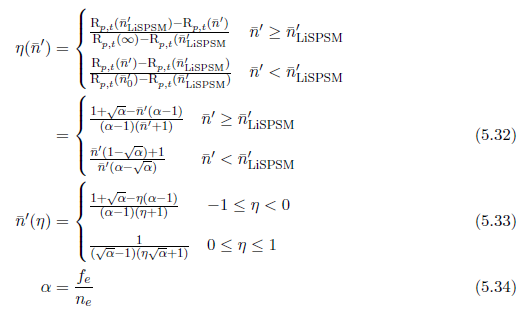
頭上のディレクショナルライトについて，\(\eta = -1\) は標準のシャドウマップに一致し，\(\eta =0\) はLiSPSMのワーピングパラメータに一致し，そして \(\eta = 1\) はPSMのワーピングパラメータに一致します。

 

5.1.2.2 Behavior over the range of warping parameters

図5.5は　\(v\) と \({\bar n}’\)，\(\eta\) によってパラメータライズされた\({\bar n}’\) の有効値すべてについての \({\tilde {\rm M}}_{p,s}\) と \({\tilde {\rm M}}_{p,t}\) を示しています。すべての \(\eta\) に対して \({\tilde {\rm M}}_{p,s}\) は \(v\) 上を単調減少します。\({\tilde {\rm M}}_{p,t}(v)\) は \(v = {\bar n}’ – {\bar n}’_0\) において内部最小値を持ち，グラフ上で示されます。\({\tilde {\rm M}}_{p,t}(v)\) は \({\bar n}’ < {\bar n}'_0\) のときに単調増加し，\({\bar n}' > {\bar n}’_0 + 1\) のときに単調減少します。\({\tilde {\rm M}}_{p,s}\) と \({\tilde {\rm M}}_{p,t}\) の最大値は境界の一点で常に存在します。ポイントライトについて，基本誤差分布は \(\cos \theta_l\) の項によって調節され（図5.1参照），境界において誤差の最大値が発生しないことを導くことを可能にします。

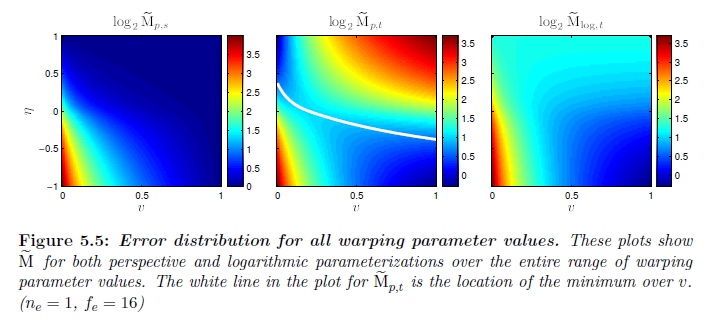
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.80 より引用。

　図5.6は図5.5の情報の一部を抽象化し，ワーピングパラメータ値の範囲上の最大誤差の振る舞いを見ることを容易にします。図は \(v=0\) と \(v=1\) の両方に対する \({\tilde {\rm M}}_{p,s}\) と \({\tilde {\rm M}}_{p,t}\) を示しています。また，\({\tilde {\rm M}}_{p,t}\) の最小値も示しています。全ての \(v\) について誤差の変化を捉えるために，これらの\(v\) の値における関数をプロットします。これらの関数の最大値は基本重要解像度因子 \(\rm R\) です。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.81 より引用。

　また，図5.6は基本ストレージ因子 \({\rm S}_p\) も示しています。\({\rm S}_p\) が最小となるためのワーピングパラメータ値がたった1つではなく，値の範囲が，すなわち \(n \in [0,1]\) で存在するということは興味深いです。これは面上であることを意味し，この範囲にあるLiSPSMsとPSMsに対するワーピングパラメータがストレージ因子の項で等価であり，少なくともディレクショナルライトに関して，\(\cos \phi_l\) 要素（グラフ上では含んでいない）は一定です。また，図5.7はポイントライトに関する最適なパラメータ値の範囲も示しています。しかしながら図5.6から，同等の範囲内でかなり変化する視錐台中で誤差の変化を見て取れます。同等の範囲上で最も大きい \({\bar n}’\) を選択すること(最も小さい \(\eta\)) は \(s\) と \(t\) 方向の間の誤差の分布が最もバランスが取れていることを保証します。この範囲上で最も小さいパラメータに関して，\({\bar n}’ = {\bar n}’_0\) であり，殆どすべての誤差は \(t\) 方向上に集中します。また，同等の範囲内で最大パラメータを選択することは，このセクションの後半で述べられるシアリングアーティファクトを減らすのに役立ちます。

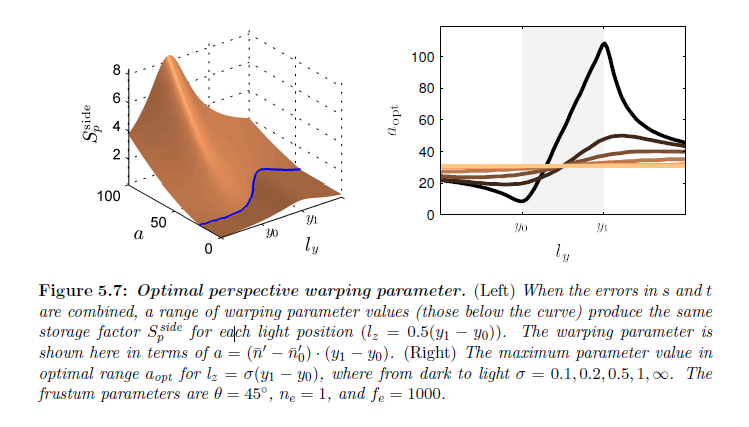
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.81 より引用。

 

5.1.2.3 Maximum error

　図5.8は最適な \(R_{p,s}\)，\(R_{p,t}\) そして面上を変化するライト位置に対する \(S_p\) を示しています。最適な \(R_{p,t}\) は次のように計算されます：
\[
\min_{{\bar n}’}{R_{p,s}} = \min_{{\bar n}’} \max_{(u,v) \in \mathcal{F}}
\left( \frac{\delta_{p,s}(u,v)}{\delta_{b,s}^{\rm side}(u,v)} \right) \tag{5.35}
\]
\(R_{p,s}\) の値は \(v=0\) における \({\tilde M}_{p,s}\) です。\(R_{p,s}\) は \({\bar n}’ = {\bar n}’_0\) のときに最小化され，\(\cos\phi_{lx} / \cos \theta\) 項のみが残ります。幾何学的には，\({\bar n}’ = {\bar n}’_0\) を設定することは利用可能な解像度の使用を最大化することで，シャドウマップ全体を埋めるために面が引き伸ばしを引き起こします。\({\bar n}’ = {\bar n}’_0\)で，\(R_{p,s}\)の項の\({\tilde {\rm M}}_{p,s}\) は定数になります。図5.7上で見られるように，\(R_{p,s}\)の最適なパラメータ\({\bar n}’\)はライトの位置で変化をします。直接的に面上にあるディレクショナルライトについて最適なパラメータ値は\({\bar n}_{\rm LiSPSM}\) です。\(v =0\) または \(v = 1\) のどちらかで最大となります。これらの頭上のディレクショナルライトについて\(s\) と \(t\) に対する最適なパラメータを用いることで，最適な\({\sf R}_p\) を得ます：
\begin{eqnarray}
\min_{{\bar n}’}{{\sf R}_{p,s}} &=& \frac{1}{\cos \theta} \tag{5.36} \\
\min_{{\bar n}’}{{\sf R}_{p,t}} &=& \frac{(f_e – n_e)}{2 \sqrt{n_e f_e}\tan \theta \cos^2 \theta} \tag{5.37} \\
& \approx & O \left( \sqrt{f_e / n_e} \right)
\end{eqnarray}
\({\bf F}_p\) が射影行列で実装された場合は，パラメータ \({\bar n}’\) は \(s\) と \(t\) に対して独立して選択することが出来ません。むしろ \(R_{p,s}\) と \(R_{p,t}\) はストレージ因子 \(S_p\) を最適化することによって同時に最適化されるべきです。頭上のディレクショナルライトについて \({\bar n}’ = {\bar n}’_{\rm LiSPSM}\) を使用することで最適な \({\sf S}_p\) を得ます：
\begin{eqnarray}
\min_{{\bar n}’}{{\sf S}_p} &=& \frac{(f_e – n_e)}{2n_e \tan\theta \cos^3 \theta} \\
&=& \frac{(f_e / n_e -1)}{2\tan\theta \cos^3\theta} \tag{5.38} \\
& \approx & O(f_e /n_e)
\end{eqnarray}
最適な透視ワーピングの効果は側面上の \({\sf S}_{un}\) から導出する\((f_e/n_e)\) を取り除くことです（式5.13参照）。\(s\) 上の最大誤差は \(F_{b,s}^{\rm side}\) と同じですが，両方の方向を同時に考慮するとき，\({\bf F}_p^{\rm side}\) の最小最大誤差の\(O(f_e /n_e)\) は \({\bf F}_b^{\rm side}\) の最大誤差の \(O(\log(f_e /n_e))\) と比較すると依然として相対的に高いです。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.83 より引用。

 

5.1.3 Logarithmic parameterization

今，ユニフォームパラメータライゼーションが端面に対して与える誤差がニアで最適な \(\delta_b\) パラメータライゼーションと同じオーダーであるということを示しました。透視パラメータライゼーションは側面上の \(s\) の方向について同じように行うことができます。対数パラメータライゼーションは \(\delta_{b,t}^{\rm side}\) に基づくパラメータライゼーションとして同じ最大誤差を得ることができます。対数パラメータライゼーションは次によって与えられます：
\[
F_{{\rm log}, t} = \frac{\log (y’/n’)}{\log (f’/n’)} \tag{5.39}
\]
これは \({\bf F}_p\) に類似したフリーなワーピングパラメータ \(n’\) を持つ対数パラメータライゼーションの一般化された形式です。\(F_{\log,t}\) によって生成された空間分布は以下になります：
\[
\delta_{\log,t} = \log(f’/n’) \frac{y’}{f’-n’} = \log \left( \frac{{\bar n}’+1}{{\bar n}’} \right) (v + {\bar n}’) \tag{5.40}
\]
ちょうど \({\tilde {\rm M}}_{p,t}\) に関して \({\tilde {\rm M}}_{\log,t}\) を計算することが可能です：
\[
{\tilde {\rm M}}_{\log,t} = \log \left( \frac{{\bar n}’+1}{{\bar n}’} \right) \frac{v + {\bar n}’}{v + {\bar n}’_0} \tag{5.41}
\]
図5.5から全パラメータ値について \(v=0\) にて最大 \({\tilde {\rm M}}_{\log,t}\) を見ることが出来ます。\(\eta = 1\) にて，\({\rm max}_v \left( {\tilde {\rm M}}_{\log, t}(v) \right)\) は最小値に達し，\(v\) 上で一定になります。

 

5.1.3.1 Maximum error

図5.9は \(R_{\log,t}\) を示しています。\(\delta_{\log,t}\) は \(\cos \theta_l\) 項に対してベストマッチしないので，ライトが面に近づいたときに \(R_{b,t}^{\rm side}\) と同じくらい低いですが，値の範囲は \(R_{b,t}^{\rm side}\) と同じ程度になります。頭上のディレクショナルライトと\({\bar n}’={\bar n}’_0\) の最適なワーピングパラメータ値で次を得ます：
\[
\min_{{\bar n}’}{{\sf R}_{\log, t}} = \frac{\log (f_e/n_e)}{2 \tan \theta \cos^2 \theta} \tag{5.42}
\]
上記は，\({\sf R}_{b,t}^{\rm side}\) と同様になります。

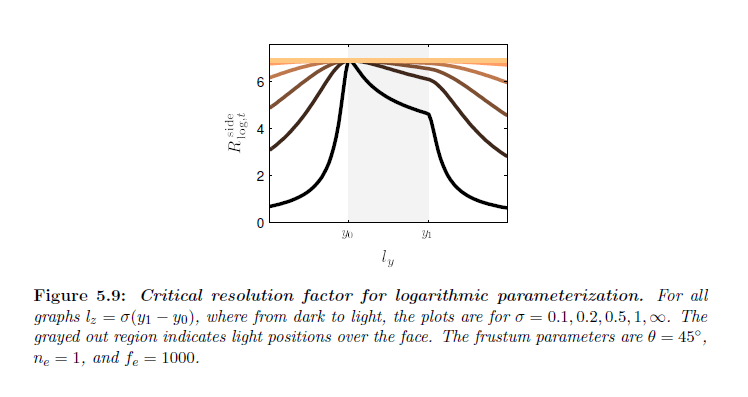
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.84 より引用。

 

5.1.4 Logarithmic + perspective parameterization

表5.3は様々なパラメータライゼーションについての誤差をまとめてあり，最後の章で導出される \(F_b\) パラメータライゼーションを含んでいます。表は，端面についてはユニフォームパラメータライゼーションを用いることで，側面上の \(s\) 方向については透視投影で，\(t\)については対数パラメータライゼーションで \(F_b\) と同じ程度の誤差であることを示しています。LogPSMパラメータライゼーションは側面上の \(s\) と \(t\) の両方に対する良い誤差範囲を得るために対数変換と透視投影を組み合わせます。

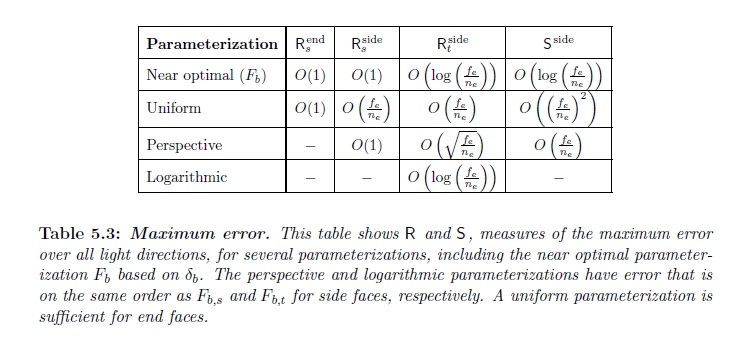
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.84 より引用。

\({\bf F}_p\) についてから始めます。\(F_{p,t}\) をある定数で乗算し，\(n’/y’\) へと変換するために別の定数を加算します。対数をとり，3つ目の定数でスケーリングすることによって \(F_{\log,t}\) を算出します。対数透視パラメータライゼーションは次によって与えられます：
\begin{eqnarray}
{\bf F}_{lp} &=& \begin{bmatrix} s \\ t \end{bmatrix} = \begin{bmatrix} F_{p,s} \\ c_0 \log (c_1 F_{p,t} + c_2) \end{bmatrix} \tag{5.43} \\
c_0 &=& \frac{-1}{\log(f’/n’)} \\
c_1 &=& \frac{n’}{p_3} = – \frac{f’-n’}{f’} \\
c_2 &=& -n’ \frac{p_2}{p_3} = 1
\end{eqnarray}
\({\bar n}’={\bar n}’_0\)で，このパラメータライゼーションは透視パラメータライゼーションと対数パラメータライゼーションそれぞれのように \(s\) と \(t\) において同程度の良い誤差範囲を提供します。図5.6上で見られるように，ディレクショナルライトに関して最適な \(S_{lp}\) は最適な \(S_p\) よりもずっと低くなります。透視パラメータライゼーションのようではなく，両方の方向に対して同じ最適なパラメータ値となります。
　\(F_{lp,t}\) についての空間分布は \(F_{\log,t}\) についてよりも一般的になります：
\begin{eqnarray}
\delta_{lp,t} &=& \frac{y’ \left( y'(c_1 p_2 + c_2) + c_1 p_3 \right) (f’ – n’)}{c_0 c_1 p_3} \tag{5.44} \\
&=& \frac{(v + {\bar n}’) \left( (v + {\bar n}’) (c_1 p_2 + c_2) + c_1 p_3 \right) W_{ly}}{c_0 c_1 p_3 } \tag{5.45}
\end{eqnarray}
\(\delta_{lp,t}\) は2つの本質的なルーツを持ちます：
\[
\lambda_0 = -{\bar n}’, {\hspace 1cm} \lambda_1 = \ – \left ( {\bar n}’ + \frac{c_1 p_3}{W_{ly} (c_1 p_2 + c_2)} \right) \tag{5.46}
\]
定数 \(c_1\) と \(c_2\) を選択した場合，\(\lambda_1 = -b\)であるので，\(\delta_{lp,t}\) を以下のように記述できます：
\[
\delta_{lp,t} \sim (v + {\bar n}’)(v + b) \tag{5.47}
\]
\(c_1\) と \(c_2\) を計算するために，必要条件 \(F_{lp,t}(0) = 0\) から追加の拘束条件が必要となります。この拘束条件は，対数の引数であるときに，\(c_1 F_{p,t}(v) + c_2\) が1であることを満たします。\(c_1\) と \(c_2\) について解くことで次を得ます：
\begin{eqnarray}
c_1 &=& -W_{ly} \frac{{\bar n}’ (b – {\bar n}’)}{{\bar n}’p_3} \tag{5.48} \\
c_1 &=& W_{ly} \frac{{\bar n}'(p_2 ({\bar n}’ – b) + p_3)}{b p_3} \tag{5.49}
\end{eqnarray}
これらの値を式5.45へと代入することで，正規化された空間分布を得ます：
\[
\delta_{lp,t} = \frac{(v + {\bar n}’)(v + b)}{c_0 ({\bar n}’ – b)} \tag{5.50}
\]
定数 \(c_0\) は拘束条件 \(F_{lp,t}(1) = 1\) から計算することが出来ます：
\[
c_0 = \frac{1}{\log \left( \frac{{\bar n}’ (b + 1)}{b({\bar n}’ + 1)} \right)} \tag{5.51}
\]
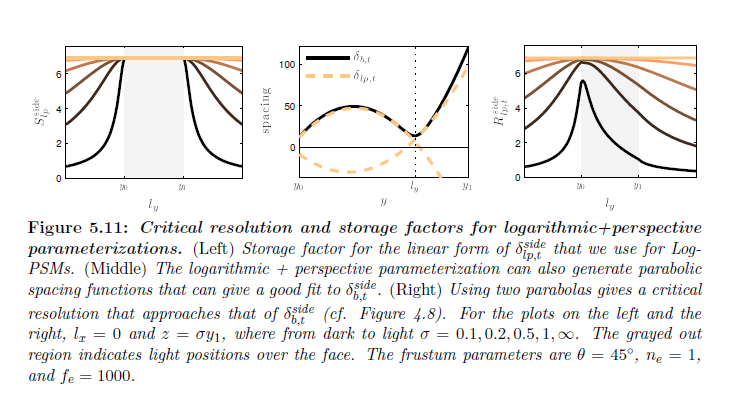
\(b \rightarrow \infty \) のとき，式5.43について示した定数は収束し，\(\delta_{lp,t}\) は線形空間分布へと収束します。図5.11は変化するライト位置に対する最小な \(S_{lp}\) してしており， \(b = \infty\) です。またパラメータ \({\bar n}’\) は \(R_{lp,s}\) に影響し，従って \(S_{lp}\) を最適化することによって \(R_{lp,t}\) と同時に最適化しなければなりません。計算上で最適なパラメータ \({\bar n}’\) を求めます。錐台の広範囲のパラメータ値とライト位置をテストすることで，最適なパラメータ値が常に \({\bar n}’ = {\bar n}’_0\) であるということがわかります（ライト位置のサブセットと\({\bar n}’\)の値についての\(S_{lp}\) は図5.10を参照)。注意してほしいのは，ライトが面上であるときに，\(R_{lp,t}\) はこのパラメータ値を持った状態で最適な\(R_{\log,t}\) よりも高くなるということです。ですが，\({\sf R}_{lp,t}\) と \({\sf R}_{\log,t}\) は同じままです。\({\sf R}_{lp,t}\) で(\({\sf R}_{p,s}\) と同じように） \({\sf R}_{lp,s}\) を乗算し，最適なワーピングパラメータ \({\bar n}’ = {\bar n}’_0\) を使用することで次を得ます：
\[
\min_{{\bar n}’}{{\sf S}_{lp}} = \frac{\log(f_e /n_e)}{2 \tan\theta\cos^3\theta} \tag{5.52}
\]

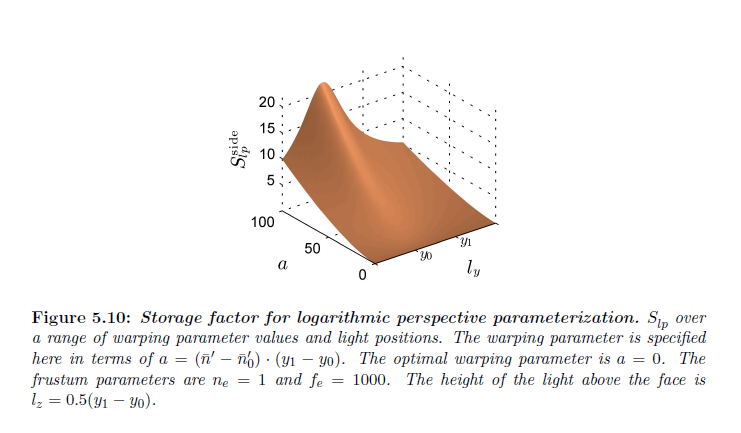
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.85 より引用。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.86 より引用。

 

5.1.4.1 Parabolic spacing functions

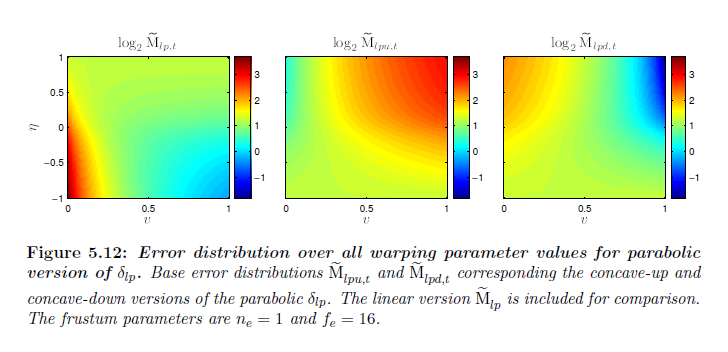
\({\bar n}’ = {\bar n}’_0\) ，\(b \neq {\bar n}’_0\) であり，\(b > 0\) または \(b < -1\) であるような有限値 \(b\) を選択することで，\(\delta_{lp}\) はパラボリックになります。\(b > {\bar n}’_0\) で，結果となるパラボラは下に凸です。\(b < {\bar n}'_0\) でパラボラは上に凸です。図5.12は下に凸と上に凸の場合に一致する基本誤差分布 \({\tilde M}_{lpu,t}\) と　\({\tilde {\rm M}}_{lpd,t}\) をそれぞれ示しています。\({\tilde {\rm M}}_{lpu,t}\) に対するワーピングパラメータ \(b\) は式5.33を用いて \(b = {\bar n}'(\eta)\) として計算されます。\({\tilde {\rm M}}_{lpd,t}\) に対するワーピングパラメータは \(b = -(1 + {\bar n}'(\eta))\) として計算されます。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.88 より引用。

2つのパラボリック空間分布関数は\(\delta_{b,t}^{\rm side}\) の湾曲した部分をより良くフィットさせるの使用することができます（図5.11参照）。しかしながら，2つのパラボラをフィッティングすることはより高価になります。なぜかというと，独立してパラメータライズされた各パーティションで面を2つの部分に分ける必要があるからです。最適な分割点 \(y_s\) は計算するのが難しいですが，\(y_s = l_y\) は最適に近い良い結果を生み出します。また図5.11は \(y_s = l_y\)，\({\bar n}’ = {\bar n}’_0\)，そして \(b\) はフリーで最小の\(S_{lp}\) を示しています。\(R_{lp,t}\) に関する曲線は \(R_{b,t}^{\rm side}\) のものと非常に類似しています。このパラメータライゼーションの1つの欠点は，各パラボラに対する最適パラメータ \(b_{\rm opt}\) について解析解が存在しないということです。それゆえ \(b_{\rm opt}\) は関係があるものを数値的に計算しなければなりません。視覚的なインパクトを探るためにこのパラメータライゼーションを用いてシャドウマップアルゴリズムを実装したいと思います。
 

5.1.5 Handling shear

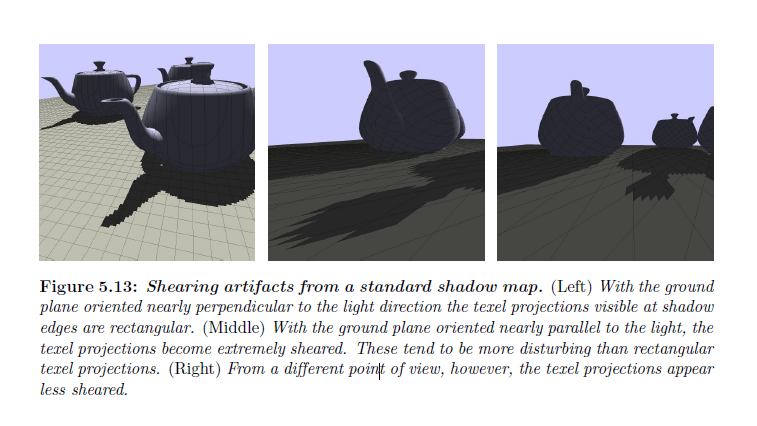
シャドウマップ解像度上の制限や，サーフェイスの向きの影響のため，常にエイリアシングアーティファクトを完全に取り除くことが可能ではありません。エイリアシングが存在する場合には，シャドウ範囲においてシーンへと個々のシャドウマップテクセルの射影を行うことが可能です。画像上のテクセルの射影の形状は3つの要因に依存します：ライトビームの横断面の形状，ビーム射影へのサーフェイスの相対方向，テクセル射影を観測する場所からの角度です。図5.13はエイリアシングが可視できるほど十分に低い解像度の標準シャドウマップを示しています。ライトビームの横断面は正方形です。ライトが直接地面上にあるときにテクセルの射影はほとんど矩形になりますが，ライトがかすめるような角度にて地面に突き当たるときには，テクセルの射影は極めてシアーします[※注1]。それらはジャギジャギな歯のように見え，より矩形の形状よりも好ましくない不自然な見た目となります。サーフェイスの向きが平行に近づくにつれて，影と影でない領域の間のコントラストがゼロに減らされるので，ディフューズシェーディングが多少役立ちます。別の視野角から，カメラが移動するにつれて，テクセルの射影はシーンに関して固定されたままになるので，テクセル射影はシアーを少なくすることが可能です。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.89 より引用。

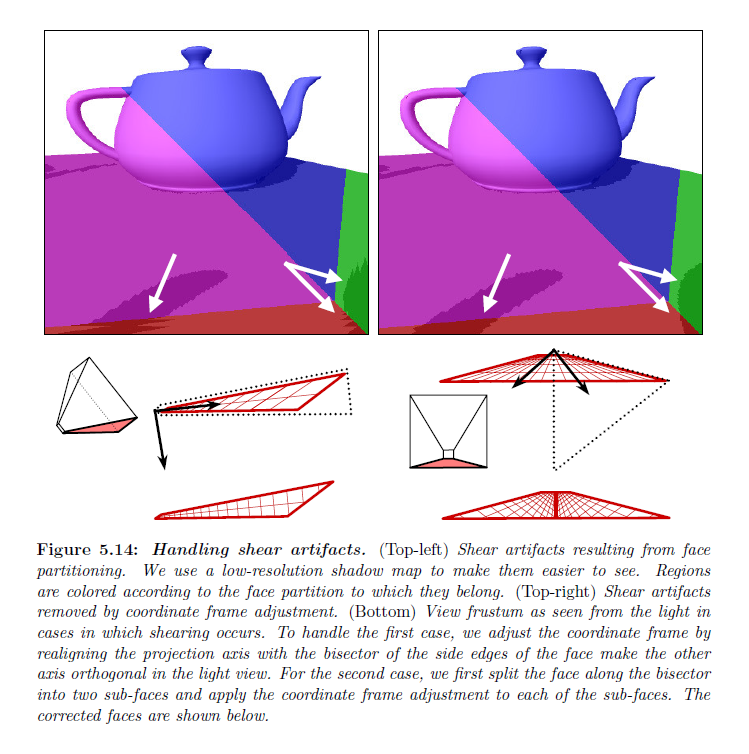
視錐台の面がパラメータライズされ，各面に対して使用されるシャドウマップのテクスチャ解像度が固定されたときに，面上のテクセルの射影はライトやカメラの位置または向きに関係なく固定されたままになります。従って，あるライト位置について，ライトビームの（ビーム方向に垂直に計測された）横断面はシアーされるようになる可能性があります。また，ワーピングそれ自身も横断面が若干シアーすることを引き起こします。面分割でシアリングは標準のシャドウマップよりも知覚なりやすくなる可能性があります。なぜかというと，同一サーフェイス上のシアリングはある面のパーティションから次のパーティションへで劇的に変化する可能性があるからです（図5.14参照）。我々の誤差尺度はこのシアリングを考慮していないので，誤差に従って解像度を再分配することはより知覚できるシアリングを作り出す可能性もまたあるかもしれません。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.90 より引用。

 

5.1.5.1 Coordinate frame adjustment

シアリングを減らすための1つの方法は面の代わりにライトに相対なパラメータライゼーションを計算することです。図5.15で示すディレクショナルライトからの側面のビューを考えます。ライトビームの横断面のシアリングはライトのビュー上における面に対してシンメトリックなワーピング錐台をフィッティングすることによって最小化することが可能です。
面の2つのサイドエッジの二等分線を持つ台形の中心線を揃えます。結果となる射影はもはやタイトではありませんが，シアリングが低減されます。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.91 より引用。

　ライト方向が側面に平行になるにつれて，ワーピング錐台によって覆われる範囲はストレージ因子の場合と同様にゼロに向かいます。しかしながら，ライト方向の小さいサブセットに関して，ワーピング錐台のファー平面からニア平面への距離比は非常に大きくなり，数値的なロバスト性の問題とライトビュー上で占めるエリアがほとんどない側面に対して高い誤差を招きます。これらを処理する1つの方法は，図5.15で示すようなワーピング錐台上の側面の一部のみを含み，除外される部分をカバーするためにニア平面を広げることです。これはわずかに全体のストレージ因子のみを増加させます。我々はこのアプローチをこの章で提示した数値結果に対してのみ使用しました。
 

5.1.5.2 \(\tau\)-limiting

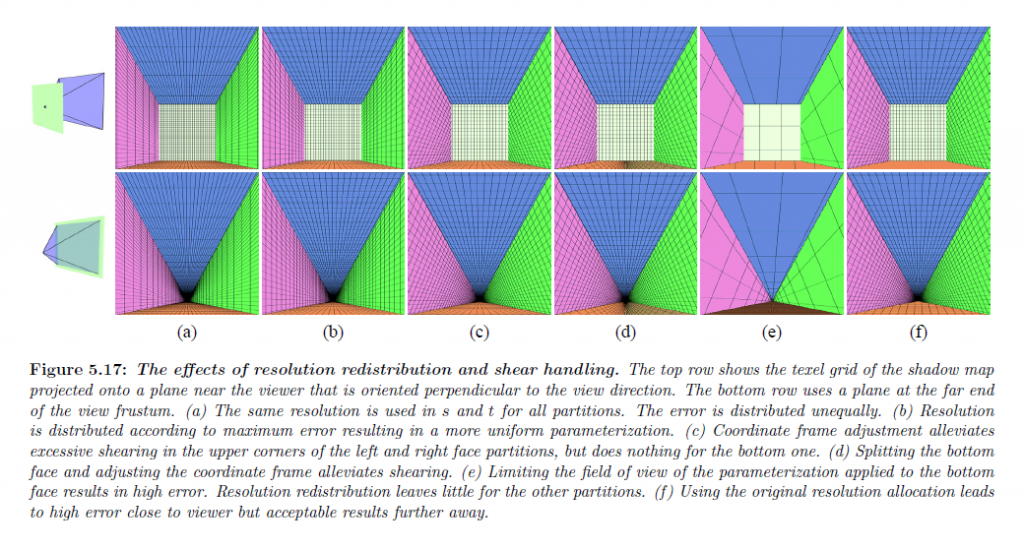
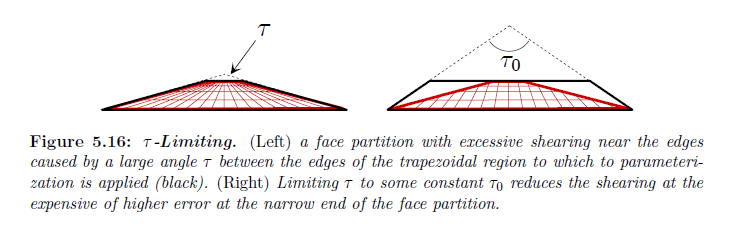
側面の2つのエッジ間の角度が大きいときに，コーディネイトフレームアジャストメントはわずかな改善を提供するかもしません（図5.17cにおける赤色面を参照）。この状況を取り扱うための1つの可能性は，ワーピング錐台のエッジ間の角度を \(\tau\) に制限して単に配置することです（図5.16参照）。このアプローチはニア平面に近い面の一部で大きな誤差を招く可能性があります。安直な解像度再分配は問題のある面に大半の解像度を割り当てます。面上の最大誤差はその他の面と均等化されますが，視錐台全体についての誤差は高くなります（図5.17e参照）。また，面に対して割り当てられた解像度を使用し，パラメータライゼーションは変化させません。観測者に近い面について，狭いフェイスパーティションの最後で誤差は極めて高くなる可能性がありますが，遠く離れた面については許容できます（図5.17f）。アプリケーションに依存するので，特にフェイスパーティションに対して視錐台の非常に小さな一部を覆うフェイスパーティションについては高い誤差状態なのでこれは問題にはならないかもしれません。妥協点は両極端のブレンドを面に対する解像度に使用することかもしれません。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.91 より引用。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.93 より引用。

 

5.1.5.3 Face splitting

大きな \(\tau\) を取り扱う別の可能性は，二等分線に沿った面を最初に分割し，それぞれ半分にコーディネイトフレームアジャストメントを適用することです。サイドエッジ間の角度 \(\tau\) が指定された閾値 \(\tau_0\) を超えたときに面を分割します。突然の切り替わりを避けるために面を分割するときに，別の閾値 \(\tau_1 > \tau_0\) を指定し，区間 \([\tau_0, \tau_1]\) について新しい座標フレームへと”イーズイン”します。\(\tau_0 > 90^\circ\) を選択することは，複数回分割される面が無いことと，2つ以上の面が同時に分割されることがないことを保証します。これは厄介な解法です。なぜかというと，ライトのビュー上で僅かな範囲を占める問題のある面を扱うために追加的なパーティションを必要とするからです。しかしながら，多くの場合においては役立ちます。
　どちらの\(\tau\) 制限も面分割を完全には満たしません。けれども，面分割と一緒にコーディネイトフレームアジャストメントを組み合わせて使用することで我々は最善の結果に達しました。後で5.3節でみるように，このスキームは全てのライト位置について必要とされるシャドウマップの数の平均値に小さな影響のみを与えます。

 

5.1.6 Total error over all light directions

これまでのところ，1つの面についての誤差を1度だけ考えてきました。面分割アルゴリズムの誤差の合計は単純に各面に対して計算されたストレージ因子を総和することによって計算することができます。
　図5.18は，半球の4分の1についてのストレージ因子の項における誤差分布を示しています（半球全体についての誤差分布はシンメトリーによって取得することが可能です）。\(F_{lp}\) は最も滑らかな誤差分布を与えます。けれども，ストレージ因子はシアリングを考慮していません。コーディネイトフレームアジャストメントを追加することとシアリングを処理するために面分割することは誤差分布においてある鋭い特徴を導入します。面分割を用いたストレージ因子上の変化はライト位置上の変化を伴って連続ですが，エントランスフェイスからイグジットフェイスへと面が変わるときに非常に急激に変化し，誤差分布上でリッジを引き起こします。しかしながら，このリッジの大きさは十分に小さくその影響はライトが周囲を動くように知覚できないものです。5.3節は面分割とその他のアルゴリズムについて全てのライト方向に対する誤差分布の追加的な解析をいくつか含んでいます。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.94 より引用。

 

5.1.7 Applying z-partitioning to faces

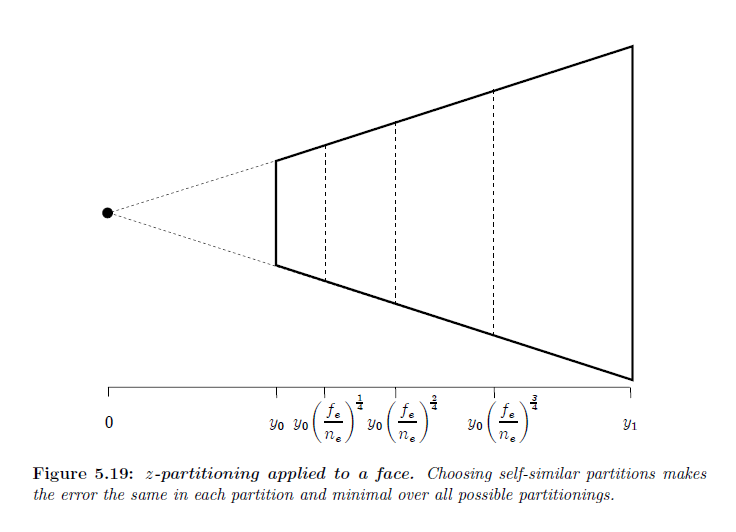
\(z\)-パーティショニングはユニフォームパラメータライゼーションと透視パラメータライゼーションに対して誤差を減らすために側面に適用することが出来ます。（この場合の面については \(y\)-パーティショニングがより適切な名前ですが，面上の \(y\)軸がアイスペースの \(z\)軸と概ね一致するので，前述の用語にこだわります。）様々な\(z\)-パーティショニングアルゴリズムとの主な違いは，パーティションが作られるところです。パーティション位置の選択は各パーティションにおいて誤差に影響を与えます。表5.3から見ることができるように，ストレージ因子（と，それゆえの誤差）は \(f_e / n_e\) で増加します。全てのパーティションにおいて最大誤差を最小化するために，そこで、各パーティションのファーからニア面までの距離比を最小化し，各パーティションの最大誤差が同じであることを確認する必要があります。\( i \in 1, 2, …, k\) に関して，分割点 \(y_{0,i}\) と \(y_{1, i}\) を選択することによって達成することができます。そのようなパーティションは（図5.19に示すように） 自己相似です：
\begin{eqnarray}
y_{0,i} &=& y_0 \left( \frac{f_e}{n_e} \right) ^{(i-1)/k} \tag{5.53} \\
y_{1,i} &=& y_{0,i+1} = y_0 \left( \frac{f_e}{n_e} \right) ^{i/k} \\
\frac{y_{1, i}}{y_{0, i}} &=& \left ( \frac{f_e}{n_e} \right) ^{1/k}
\end{eqnarray}
この\(z\)-パーティショニングスキームは，\(n’ = n_e\) で，対数パラメータライゼーションの離散的な近似として見ることができます。このワーピングパラメータを用いて，\(F_{\rm log}^{\rm side}\) の逆関数 \(G_{\rm log}^{\rm side}\) は次のように与えられます：
\[
G_{\rm log}^{\rm side}(t) = y_0 \left( \frac{f_e}{n_e} \right) ^ t \tag{5.54}
\]
シャドウマップの領域 \(t\) を \(k\) 等分することは，式5.53によって計算される面上に対応するパーティションを生成します。このパーティショニングスキームを \(\sf ZP_{log}\) と示します。これらの分割位置を持つユニフォームパラメータライゼーションと透視パラメータライゼーションに対する最適な最大ストレージ因子は \(f_e/n_e\) の代わりに \(y_{1,i}/y_{0,i}\) を用いて式5.13と5.38から計算することができます：
\begin{eqnarray}
{\sf S}^{\rm side}_{un, k} &=& \sum_{i=1}^{k} (y_{1,i}/y_{0,i}) \frac{((y_{1, i}/y_{0, i})-1)}{2 \tan \theta \cos^3 \theta} \\
&=& k (f_e / n_e)^{1/k} \frac{((f_e / n_e)^{1/k} – 1)}{2 \tan \theta \cos^3 \theta} \tag{5.55} \\
{\sf S}^{\rm side}_{p,k} &=& \sum_{i=1}^{k} \frac{((y_{1, i}/y_{0, i}) -1)}{2 \tan \theta \cos^3 \theta } \\
&=& k \frac{(f_e/n_e)^{1/k}-1}{2 \tan\theta \cos^3\theta} \tag{5.56}
\end{eqnarray}
分割が隣接している限り（すなわち，\(y_{0,i+1} = y_{1, i}\)），対数透視パラメータライゼーションは実は使用されるパーティショニングスキームに無関係です。式5.52から次を得ます：
\begin{eqnarray}
{\sf S}^{\rm side}_{lp, k} &=& \frac{1}{2 \tan\theta \cos^3\theta} \sum_{i=1}^{k} \log (y_{1, i}/y_{0, i}) \\
&=& \frac{1}{2 \tan\theta \cos^3\theta} \sum_{i=1}^{k} \log(y_{0, i+1}) – \log(y_{0, i}) \\
&=& \frac{1}{2 \tan\theta\cos^3\theta} \left( \log(y_{0, k+1}) – \log(y_{0, 1}) \right) \\
&=& \frac{\log (f_e/n_e)}{2 \tan\theta\cos^3\theta} = {\sf S}^{\rm side}_{lp} \tag{5.57}
\end{eqnarray}
パーティションの数が増加するにつれて，\({\sf S}^{\rm side}_{un,k}\) と \({\sf S}^{\rm side}_{p,k}\) は　\({\sf S}^{\rm side}_{lp}\) へと収束します。極限 \(\displaystyle \lim_{k \to \infty}{\sf S}^{\rm side}_{p,k}\) は不定形 \(\infty ・ 0\) を生み出します。商として \({\sf S}^{\rm side}_{p,k}\) を書き直し，ロピタルの定理を適用することで次を得ます：
\begin{eqnarray}
\lim_{k \to \infty} k \frac{(f_e/n_e)^{1/k}-1}{2 \tan\theta\cos^3\theta} &=& \lim_{k \to \infty} \frac{(f_e/n_e)^{1/k}-1}{2/k\tan\theta\cos^3\theta} \\
&=& \lim_{k \to \infty} \frac{ \frac{-(f_e/n_e)^{1/k}\log(f_e/n_e)}{k^2}}{-2/k^2\tan\theta\cos^3\theta} \\
&=& \frac{\log(f_e/n_e)}{2\tan\theta\cos^3\theta}
\end{eqnarray}
極限 \(\displaystyle \lim_{k \to \infty}{\sf S}^{\rm side}_{un,k}\) は同様に計算することができます。
　Zhangら(2006)は平行分割シャドウマップ(PSSMs)に対して線形パーティショニングスキームと \({\sf ZP_{log}}\) を組み合わせて使用しました。線形パーティショニングスキーム \({\sf ZP_{lin}}\) はユニフォームな幅のパーティションを生成します：
\begin{eqnarray}
y_{0,i}^{\sf lin} &=& y_0 + (y_1 – y_0) \frac{i-1}{k} \tag{5.58} \\
y_{1,i}^{\sf lin} &=& y_{0, i+1} = y_0 + (y_1 – y_0) \frac{i}{k} \tag{5.59}
\end{eqnarray}
PSSMスキーム \({\sf ZP_{PSSM}}\) は \({\sf ZP_{log}}\) と \({\sf ZP_{lin}}\) について分割位置の平均を取ります：
\begin{eqnarray}
y_{0,i}^{\sf PSSM} &=& \frac{y_{0,i}^{\sf lin} + y_{0,i}^{\sf log}}{2} \tag{5.60} \\
y_{1,i}^{\sf PSSM} &=& \frac{y_{1,i}^{\sf lin} + y_{1,i}^{\sf log}}{2} \tag{5.61}
\end{eqnarray}
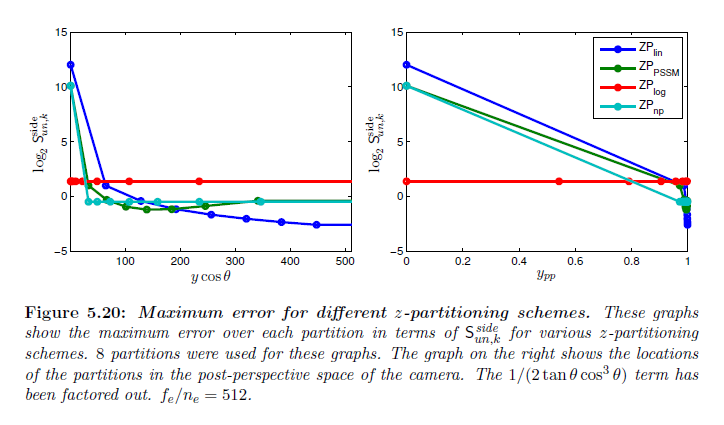
図5.20は，これらの\(z\)-パーティショニングスキームについての誤差を示しています。\({\sf ZP_{PSSM}}\) は遠く離れた領域を優先して観測者に近い部分が高い誤差になるのをトレードオフします。観測者に近い領域はワールド空間上では小さな部分を占めるだけですが，透視変換後の空間のカメラにおいてはそれらの領域は視錐台の大部分を占めます。したがって，同様にして画像の大部分を占めます。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.95 より引用。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.98 より引用。

 

5.1.7.1 Continuity

ライト位置が変わるにつれて，面上の誤差もまた変化します。適応的に\(z\)-パーティショニングを適用すること，すなわち高い誤差を持つ面に対してのみ使用することは魅力的かもしれません。けれども，シャドウマップの解像度が十分に高くない場合に，フレームからフレームへの変化する \(z\)-パーティションの数は，テンポラルアーティファクトを引き起こす可能性があります。なぜかというと，エイリアシング誤差の分布上で突然のシフトが引き起こるからです。一般には，すべての面とライト方向についてポッピングを避けるために同じ数の\(z\)-パーティションを使用するのが最も良いです。ある状況においては，幅ゼロのパーティションを導入し，複数フレームにわたって新しい位置へと分割位置をモーフィングすることによってポッピングなしで\(z\)-パーティションを追加することが可能かもしれません。ですが，我々はこれを試しませんでした。
 

5.1.8 A \(z\)-patitioning scheme using a pseudo-near plane

\({\sf ZP_{PSSM}}\) の理論的根拠は，観測者に近い領域がしばしば空になるということです。この場合に，最も良い方法は，視錐台のニア平面距離を増加させることです。たとえ \(n_e\) において小さな増加であっても，誤差を劇的に減らせる可能性があります。けれども，\(n_e\) 上のタイトな上限値を計算することは高価です。なぜかというと，視錐台に対してジオメトリのクリッピングを含む可能性があるからです。それゆえ，ジオメトリのニア平面クリッピングを避けるために，\(n_e\) へ伝統的に低い値を設定するのが一般的です。\(\sf ZP_{PSSM}\) のようなアプローチは，視錐台の中間範囲について誤差が低い状態を保つ間，\(n_e\)　の小さな値を使用することができます。あるサーフェイスが実際に領域に侵入することが発生した際に観測者に近い領域についてシャドウマップ範囲が与えられますが，ここにおいては誤差は高いかもしれません。
　シーンを占有する可能性がある錐台の一部についての情報を提供するために 擬似ニア平面 を使用する代替アプローチを提案します。これは，エイリアシング誤差を低く保ちながら伝統的な \(n_e\) をまだ使用することができます。支払われるべき代価となる \(n_e\) と擬似ニア平面距離 \(n_p\) との間の誤差は高くなる可能性があります。側面について，\(n_p\) に一致する点は \(y_{np} = n_p / \cos\theta\) です。以下に従い，分割位置を計算します：

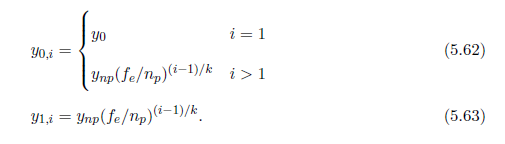
\(\sf ZP_{np}\) としてこのスキームを示します。\(n_p = y_{1,1}^{\sf PSSM}\cos\theta\) を設定した場合は，\(\sf ZP_{PSSM}\) として最初のパーティションに同じ最大誤差を得ますが，後のパーティションについて最大誤差は \(\sf ZP_{PSSM}\) のパーティションに一致するものよりも低いです（図5.20参照）。
　単一のパーティショニングスキームはすべてのアプリケーションの要求を満たすことができないので，、ユーザが望む誤差分布を達成するために、図5.20と同様のグラフで対話的に分割点を操作することを可能にするツールを開発したいです。また、可能な限り厳密にユーザーが指定した誤差プロファイルに一致するように自動的にパーティションを作成する可能性を模索したいと思います。
 

5.1.9 Warping algorithm using a pseudo-near plane

\(\sf ZP_{np}\) と同じ考えで，擬似ニア平面を使用するワーピングアルゴリズムを定式化することができます。このアルゴリズムに対して，我々は \(v > v_{np}\) である面上の一部について最大誤差を最小化します。ここで，\(v_{np} \in [0,1]\) は擬似ニア平面の位置です。図5.21は与えられた \(v_{np}\) について最小となる \(\rm S\) を生み出すワーピングパラメータ値についてのカーブと同様のちょうど\([v_{np}, 1]\) の範囲について変化する \(v_{np}\) についての \(\rm S\) を示しています。最初は，0から \(v_{np}\) が増加するにつれて，透視パラメータライゼーションの結果として最適な \(\bar n’\) は擬似ニア平面とファー平面において同じ誤差となります。従って，\(\bar n’\) は \(v = v_{np}\) と \(v=1\) の互いに等しい \({\tilde {\rm M}}_{p,t}\) の値を算出する \({\bar n}’\) について解くことで \({\bar n}’_{\rm LiSPSM}\) と同様の方法で見つけることができます：
\[
{\bar n}’_{\rm opt} = {\bar n}’_0 + \sqrt{({\bar n}’_0 + v_{np})({\bar n}’_0 + 1)} \tag{5.64}
\]
\(v_{np}\) が増加し続けるのと同じように，\(\bar n’\) も増加し続けます。ある点において最適な最大誤差は \(v_{np}\) においてのみ求まり，ファー平面においては求まりません。この点で，式5.64が算出する値は非常に小さいです。このとき，最適な \(\bar n’\) は　\(\bar n’\) について \({\rm dS}_p(v_{np})/{\rm d}{\bar n}’ = 0\) を解くことによって求まります。3つの解を求めると，\(-v_{np}\) の2重根は\({\bar n}’ > {\bar n}’_0\) の拘束条件のため無効であるので，3重根が正しい解となります：
\[
{\bar n}’_{\rm opt} = \frac{v_{np}}{2 – 3 v_{np}} \tag{5.65}
\]
\(v_{np}\) が \(2/3\) へと増加し続けるにつれて，\({\bar n}’_{\rm opt}\) は無限大へと近づきます。\(v_{np} = 2/3\) を超えると，\({\bar n}’_{\rm opt}\) は無限大のままです。\(v_{np} < 2/3\) について，式5.64と5.65の最大値を取ることによって単純に \({\bar n}'_{\rm opt}\) を決めます。

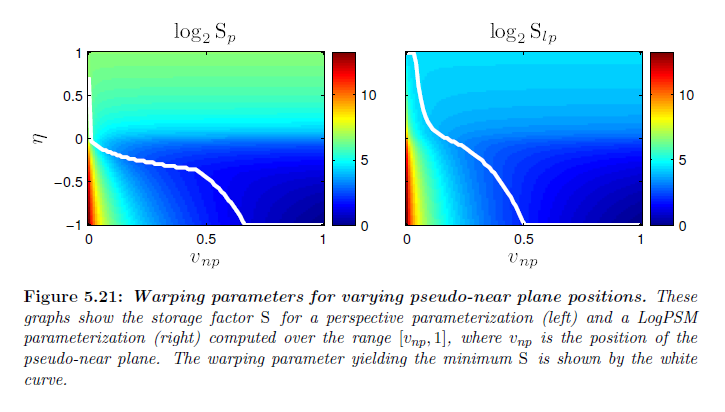
※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.100 より引用。

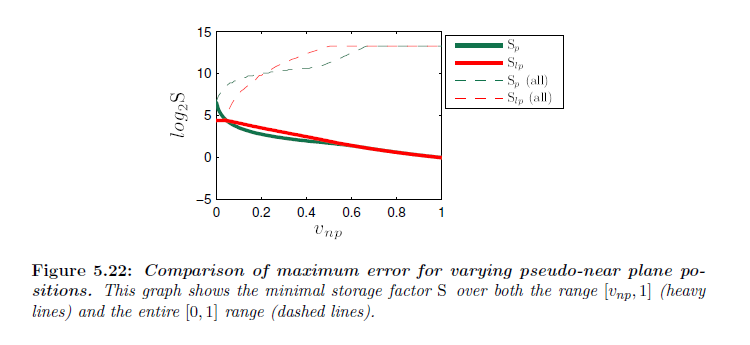
　類似したアルゴリズムは範囲 \([v_{np}, 1]\) について計算される \({\rm S}_{lp}\) を最小化する \({\bar n}’_{\rm opt}\) を求めることによってLogPSMパラメータライゼーションを用いて定式化することが可能です。しかしながら，\({\rm dS}_{lp}(v_{np})/{\rm d}{\bar n}’ = 0\) は解析解を持たず，数値的に解く必要があります。これを行う１つの可能な方法は最適な \(\eta\) を求めるために囲い込み最小化法（例．黄金分割探索 (Pressら, 1992)）を使用して，\(\eta\) で \({\rm S}_{lp}\) をパラメータライズすることです。図5.22は，透視とLogPSMパラメータライゼーションの両方を用いたときの最大誤差を比較しています。全体的に，グラフは非常に似ています。図5.23はLiSPSMアルゴリズムとワーピングパラメータを計算するために擬似ニア平面を用いた透視ワーピングアルゴリズム間の比較を示しています。シーンが視錐台の位置のみを占有するので，観測者から遠く離れた擬似ニア平面を設定することによって低い誤差を得ることが可能です。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.100 より引用。

※図はLloyd, B. 2007. Logarithmic perspective shadow maps. PhD thesis, University of North Carolina. p.102 より引用。

 

---

注1：シアー（shear）。要するに，刈り取りされてシャドウマップが毛羽立ったようになってジャギること。図5.13のような状態。